题目内容
1.口袋A中有2个相同的小球,分别写有数字3,6,口袋B中有4个相同的小球,分别写有数字3,4,5,6,在口袋B中随机地抽出一个小球放入口袋A中.求以口袋A中的3个小球上的数字为边能构成等腰三角形的可能性大小.分析 根据题意得出所有的可能,进而求出答案.
解答 解:由题意可得:3,3,6无法构成三角形,
3,6,4不是等腰三角形;
3,6,5不是等腰三角形;
3,6,6是等腰三角形,
故能构成等腰三角形的概率为:$\frac{1}{4}$.
点评 此题主要考查了可能性大小,正确求出事件发生的概率是解题关键.

练习册系列答案
相关题目
6.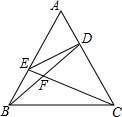 如图所示,正三角形ABC的边长为2,$\frac{AE}{BE}$=2,$\frac{AD}{DC}$=$\frac{1}{2}$,BD交CE于点F,则△AEF的外接圆半径长为( )
如图所示,正三角形ABC的边长为2,$\frac{AE}{BE}$=2,$\frac{AD}{DC}$=$\frac{1}{2}$,BD交CE于点F,则△AEF的外接圆半径长为( )
 如图所示,正三角形ABC的边长为2,$\frac{AE}{BE}$=2,$\frac{AD}{DC}$=$\frac{1}{2}$,BD交CE于点F,则△AEF的外接圆半径长为( )
如图所示,正三角形ABC的边长为2,$\frac{AE}{BE}$=2,$\frac{AD}{DC}$=$\frac{1}{2}$,BD交CE于点F,则△AEF的外接圆半径长为( )| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{3}}{7}$ |
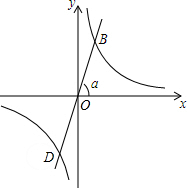 如图,正比例函数的图象与x轴正方向所成角为α度,若它与反比例函数y=$\frac{\sqrt{3}}{x}$的图象分别交于第一、三象限的点B和点D.
如图,正比例函数的图象与x轴正方向所成角为α度,若它与反比例函数y=$\frac{\sqrt{3}}{x}$的图象分别交于第一、三象限的点B和点D.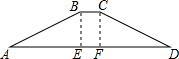 如图,为消除淮河灾害,某市水利部门修建了横断面是梯形的淮河大坝,坝顶宽6米,坝高BE=CF=20米,斜坡AB的坡角∠A=30°,斜坡CD的坡度i=1:3,(坡度是指坡面的铅直高度与水平宽度的比).求坝底AD的宽.(结果保留整数,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,为消除淮河灾害,某市水利部门修建了横断面是梯形的淮河大坝,坝顶宽6米,坝高BE=CF=20米,斜坡AB的坡角∠A=30°,斜坡CD的坡度i=1:3,(坡度是指坡面的铅直高度与水平宽度的比).求坝底AD的宽.(结果保留整数,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)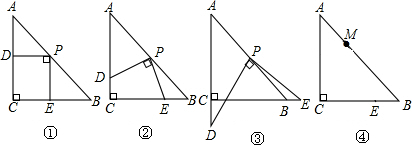
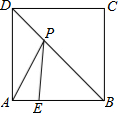 如图,E为正方形ABCD边AB上一点,BE=3,AE=1,P为对角线BD上一个动点,则PA+PE的最小值是5(正方形的四条边相等,四个角是直角)
如图,E为正方形ABCD边AB上一点,BE=3,AE=1,P为对角线BD上一个动点,则PA+PE的最小值是5(正方形的四条边相等,四个角是直角)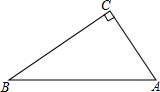 如图,已知△ABC中,∠ACB=90°,AC=3,BC=5,M为AB的中点.
如图,已知△ABC中,∠ACB=90°,AC=3,BC=5,M为AB的中点.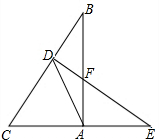 如图,△ABC中,∠BAC=90°,点D为BC上一点,且∠C=∠DAC,DE⊥BC交AB于F,交CA的延长线于E.
如图,△ABC中,∠BAC=90°,点D为BC上一点,且∠C=∠DAC,DE⊥BC交AB于F,交CA的延长线于E.