题目内容
 如图:△ABC中,AB=6cm,BC=8cm,∠B=90°,点P从A点开始沿AB边向点B以1厘米/秒的速度移动,点Q从B点开始沿BC边向C以2厘米/秒的速度移动.
如图:△ABC中,AB=6cm,BC=8cm,∠B=90°,点P从A点开始沿AB边向点B以1厘米/秒的速度移动,点Q从B点开始沿BC边向C以2厘米/秒的速度移动.(1)如果P、Q分别从A、B两点同时出发,经几秒钟,使△PBQ的面积等于8cm2?
(2)如果P、Q分别从A、B两点同时出发,并且P到B后又继续在BC上前进,Q点到C点后又继续在CA边上前进,当P在BC上,Q在AC上时,是否存在某一时刻,使△PCQ的面积等于12.6cm2?若存在求运动时间;若不存在,请说明理由.
考点:一元二次方程的应用
专题:几何动点问题
分析:(1)设x秒时.由三角形的面积公式列出关于x的方程,
(6-x)•2x=8,通过解方程求得x1=2,x2=4;
(2)过Q作QD⊥CB,垂足为D,构建相似三角形△CQD∽△CAB,由该相似三角形的对应边成比例得到
=
,QD=
;
然后由三角形的面积公式列出关于x的方程
(14-x)•
=12.6,解之得x1=7,x2=11.由实际情况出发,来对方程的解进行取舍.
| 1 |
| 2 |
(2)过Q作QD⊥CB,垂足为D,构建相似三角形△CQD∽△CAB,由该相似三角形的对应边成比例得到
| QD |
| 2x-8 |
| AB |
| AC |
| 6(2x-8) |
| 10 |
然后由三角形的面积公式列出关于x的方程
| 1 |
| 2 |
| 6(2x-8) |
| 10 |
解答:解:(1)设x秒时,点P在AB上,点Q在BC上,且使△PBQ面积为8cm2,
由题意得
(6-x)•2x=8,解之,得x1=2,x2=4,
经过2秒时,点P到距离B点4cm处,点Q到距离B点4cm处;
或经4秒,点P到距离B点2cm处,点Q到距离B点8cm处,△PBQ的面积为8cm2,
综上所述,经过2秒或4秒,△PBQ的面积为8cm2;
(2)当P在AB上时,经x秒,△PCQ的面积为:
×PB×CQ=
×(6-x)(8-2x)=12.6,
解得:x1=
(不合题意舍去),x2=
,
经x秒,点P移动到BC上,且有CP=(14-x)cm,点Q移动到CA上,且使CQ=(2x-8)cm,
过Q作QD⊥CB,垂足为D,由△CQD∽△CAB得
=
,
即 QD=
,
由题意得
(14-x)•
=12.6,解之得x1=7,x2=11.
经7秒,点P在BC上距离C点7cm处,点Q在CA上距离C点6cm处,使△PCQ的面积等于12.6cm2.
经11秒,点P在BC上距离C点3cm处,点Q在CA上距离C点14cm处,14>10,点Q已超出CA的范围,此解不存在.
综上所述,经过7秒和
秒时△PCQ的面积等于12.6cm2.
由题意得
| 1 |
| 2 |
经过2秒时,点P到距离B点4cm处,点Q到距离B点4cm处;
或经4秒,点P到距离B点2cm处,点Q到距离B点8cm处,△PBQ的面积为8cm2,
综上所述,经过2秒或4秒,△PBQ的面积为8cm2;
(2)当P在AB上时,经x秒,△PCQ的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
解得:x1=
25+2
| ||
| 5 |
25-2
| ||
| 5 |
经x秒,点P移动到BC上,且有CP=(14-x)cm,点Q移动到CA上,且使CQ=(2x-8)cm,
过Q作QD⊥CB,垂足为D,由△CQD∽△CAB得
| QD |
| 2x-8 |
| AB |
| AC |
即 QD=
| 6(2x-8) |
| 10 |
由题意得
| 1 |
| 2 |
| 6(2x-8) |
| 10 |
经7秒,点P在BC上距离C点7cm处,点Q在CA上距离C点6cm处,使△PCQ的面积等于12.6cm2.
经11秒,点P在BC上距离C点3cm处,点Q在CA上距离C点14cm处,14>10,点Q已超出CA的范围,此解不存在.
综上所述,经过7秒和
25-2
| ||
| 5 |
点评:本题考查了相似三角形的判定与性质以及一元二次方程的应用.灵活运用面积公式,列出方程,正确理解两解,合理取合.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案
相关题目
 如图,边长为1的正△ABC,沿EF折叠,使B点落在AC上的点H处,且FH⊥AC,求折成的四边形AEFC的面积.
如图,边长为1的正△ABC,沿EF折叠,使B点落在AC上的点H处,且FH⊥AC,求折成的四边形AEFC的面积.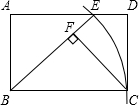 如图,在矩形ABCD中,AB=3,BC=5,以顶点B为圆心,边BC长为半径画弧,交AD边于点E,连结BE,过C点作CF⊥BE于F.
如图,在矩形ABCD中,AB=3,BC=5,以顶点B为圆心,边BC长为半径画弧,交AD边于点E,连结BE,过C点作CF⊥BE于F. 如图,△ABC在方格纸中
如图,△ABC在方格纸中 在第一象限内作射线OC,与x轴的夹角为60°,在射线OC上取一点A,过点A作AH⊥x轴于点H,在抛物线y=x2(x>0)上取一点P,在y轴上取一点Q,使得以P、O、Q为顶点的三角形与△AOH全等,则符合条件的点A的坐标是
在第一象限内作射线OC,与x轴的夹角为60°,在射线OC上取一点A,过点A作AH⊥x轴于点H,在抛物线y=x2(x>0)上取一点P,在y轴上取一点Q,使得以P、O、Q为顶点的三角形与△AOH全等,则符合条件的点A的坐标是