题目内容
9.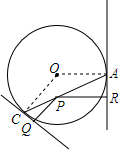 如图,设P为圆O内一定点,过P任作一弦AC,分别过A,C引圆的切线,再过P分别作两切线的垂线,垂足为Q,R.求证:$\frac{1}{PQ}$+$\frac{1}{PR}$为定值.
如图,设P为圆O内一定点,过P任作一弦AC,分别过A,C引圆的切线,再过P分别作两切线的垂线,垂足为Q,R.求证:$\frac{1}{PQ}$+$\frac{1}{PR}$为定值.
分析 过点A作直径交⊙O于点E,连接EC,通过相似三角形△AEC∽△PAR,得出关于AC,PQ,AE,AP的比例关系式,同理可求出AC,PR,AE,PC的比例关系式,两式联立可得出$\frac{1}{PQ}$+$\frac{1}{PR}$ 的表达式,然后根据相交弦定理即可证得所求的结论.
解答 证明:过点A作直径交⊙O于点E,连接EC,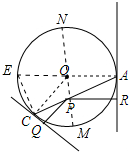 过P作直径交⊙O于M,N,
过P作直径交⊙O于M,N,
∴∠ECA=90°.
∵AE⊥AR,PR⊥AR,
∴AE∥PR且∠PRA=90°.
∴∠EAC=∠APR,∠ACE=∠PRA,
∴△AEC∽△PAR.
∴$\frac{AC}{PR}$=$\frac{AE}{PA}$ ①
同理可得:$\frac{AC}{PQ}$=$\frac{AE}{PC}$②
①+②,得:$\frac{AC}{PR}$+$\frac{AC}{PQ}$=$\frac{AE}{PA}$+$\frac{AE}{PC}$
∴$\frac{1}{PQ}$+$\frac{1}{PR}$=$\frac{AE}{AC}$•$\frac{PA+PC}{PA•PC}$=$\frac{AE}{PA•PC}$,
∵PA•PC=PM•PN.
∴$\frac{1}{PQ}$+$\frac{1}{PR}$=$\frac{AE}{PM•PN}$.
∵AE是直径,点P是定点,
∴PM•PN是定值,
∴$\frac{1}{PQ}$+$\frac{1}{PR}$是定值.
点评 本题主要考查了相似三角形和相交弦定理的应用,根据相似三角形得出与所求相关的线段成比例是解题的关键,题目有一定难度,学会条件常用辅助线,构造相似三角形.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
3. 如图,点O是△ABC的内心,∠A=62°,则∠BOC=( )
如图,点O是△ABC的内心,∠A=62°,则∠BOC=( )
 如图,点O是△ABC的内心,∠A=62°,则∠BOC=( )
如图,点O是△ABC的内心,∠A=62°,则∠BOC=( )| A. | 59° | B. | 31° | C. | 124° | D. | 121° |
18.数轴上表示1,$\sqrt{2}$的对应点分别为A、B.点B关于点A的对称点为C,则点C所表示的相反数是( )
| A. | -1-$\sqrt{2}$ | B. | 1-$\sqrt{2}$ | C. | -2+$\sqrt{2}$ | D. | -2-$\sqrt{2}$ |
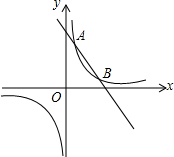 如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象相交于点A(2,5)和B,并且点A与点B关于第一、三象限的角平分线对称.
如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象相交于点A(2,5)和B,并且点A与点B关于第一、三象限的角平分线对称. 如图,已知长方形ABCD的两边长为AB=6,BC=4,将矩形ABCD绕着点C顺时针旋转90°后,点A转到点A′的位置上,对角线AC扫过的面积是13π.
如图,已知长方形ABCD的两边长为AB=6,BC=4,将矩形ABCD绕着点C顺时针旋转90°后,点A转到点A′的位置上,对角线AC扫过的面积是13π.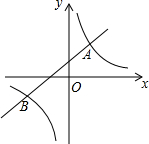 如图,直线y=kx+b(k≠0)与双曲线y=$\frac{m}{x}$(m≠0)相交于A(1,2),B(n,-1)两点.
如图,直线y=kx+b(k≠0)与双曲线y=$\frac{m}{x}$(m≠0)相交于A(1,2),B(n,-1)两点.