题目内容
19.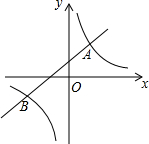 如图,直线y=kx+b(k≠0)与双曲线y=$\frac{m}{x}$(m≠0)相交于A(1,2),B(n,-1)两点.
如图,直线y=kx+b(k≠0)与双曲线y=$\frac{m}{x}$(m≠0)相交于A(1,2),B(n,-1)两点.(1)求双曲线的解析式;
(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<0<x2<x3,请直接写出y1,y2,y3的大小关系;
(3)观察图象,请直接写出不等式kx+b<$\frac{m}{x}$的解集.
分析 (1)根据待定系数法即可求得;
(2)根据反比例函数的性质即可判断;
(3)根据图象的交点坐标即可得到不等式kx+b<$\frac{m}{x}$的解集.
解答 解(1 )∵双曲线y=$\frac{m}{x}$经过点A(1,2),
∴m=2,
∴双曲线的解析式为y=$\frac{2}{x}$;
(2)根据反比例函数的图象在一、三象限y随x的增大而减小可知:若x1<0<x2<x3,则y2>y3>y1;
(3)∵点B(n,-1)在双曲线y=$\frac{2}{x}$上,
∴n=-2,
∴B点坐标为(-2,-1)
A(1,2)、B(-2,-1)在直线y=kx+b上,
∴$\left\{\begin{array}{l}{k+b=2}\\{-2k+b=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$.
∴直线的解析式为y=x+1.
根据图象得当x<-2或0<x<1时,kx+b<$\frac{m}{x}$,
即不等式kx+b<$\frac{m}{x}$的解集为:x<-2或0<x<1.
点评 本题考查了反比例函数和一次函数的交点问题,解题的关键是熟练掌握待定系数法和反比例函数的性质.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
7.长春市总面积为20565平方公里,20565这个数用科学记数法表示为( )
| A. | 20.565×102 | B. | 2.0565×103 | C. | 2.0565×104 | D. | 0.20565×104 |
11.如果∠1与∠2的两边互相平行,那么这两个角( )
| A. | 相等 | B. | 互补 | C. | 相等或互补 | D. | 无法确定 |
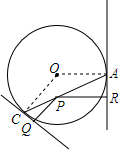 如图,设P为圆O内一定点,过P任作一弦AC,分别过A,C引圆的切线,再过P分别作两切线的垂线,垂足为Q,R.求证:$\frac{1}{PQ}$+$\frac{1}{PR}$为定值.
如图,设P为圆O内一定点,过P任作一弦AC,分别过A,C引圆的切线,再过P分别作两切线的垂线,垂足为Q,R.求证:$\frac{1}{PQ}$+$\frac{1}{PR}$为定值. 如图,在等腰直角三角形ABC中,∠ACB=90°,AB=4,以点A为圆心,AC长为半径作弧,交AB于点D,则图中阴影部分面积为4-π.
如图,在等腰直角三角形ABC中,∠ACB=90°,AB=4,以点A为圆心,AC长为半径作弧,交AB于点D,则图中阴影部分面积为4-π.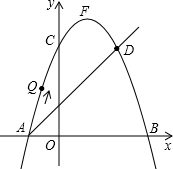 如图,在平面直角坐标系中,直线AD与抛物线y=-x2+bx+c交于A(-1,0)和D(2,3)两点,点C、F分别为该抛物线与y轴的交点和顶点.
如图,在平面直角坐标系中,直线AD与抛物线y=-x2+bx+c交于A(-1,0)和D(2,3)两点,点C、F分别为该抛物线与y轴的交点和顶点. 如图,在菱形ABCD中,∠B=60°,AB=2,扇形AEF的半径为2,圆心角为60°,则阴影部分的面积是$\frac{2}{3}π$-$\sqrt{3}$.
如图,在菱形ABCD中,∠B=60°,AB=2,扇形AEF的半径为2,圆心角为60°,则阴影部分的面积是$\frac{2}{3}π$-$\sqrt{3}$.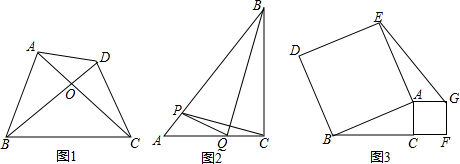
 如图,在△ABC中,AB=AC=6,BC=4,⊙B与边AB相交于点D,与边BC相交于点E,设⊙B的半径为x.
如图,在△ABC中,AB=AC=6,BC=4,⊙B与边AB相交于点D,与边BC相交于点E,设⊙B的半径为x.