题目内容
1.解下列不等式,并把解集在数轴上表示出来.(1)$\frac{2x-1}{3}$≤$\frac{3x-4}{6}$;
(2)$\frac{5x+1}{6}$-2>$\frac{2x-5}{6}$;
(3)$\frac{3-x}{2}$≤1-$\frac{2x-5}{6}$;
(4)3+$\frac{2-3x}{5}$≥$\frac{x+1}{2}$.
分析 利用不等式的基本性质:去分母,去括号,移项,合并同类项,系数化1,分别把它们解出来,再在数轴上表示出来.
解答 解:(1)去分母得:2(2x-1)≤3x-4,
去括号得:4x-2≤3x-4,
移项,合并得:x≤-2,
解集表示在数轴上如图:
(2)去分母得:5x+1-12>2x-5,
移项、合并得:3x>6,
系数化为1得:x>2,
(3)去分母得:3(3-x)≤6-(2x-5),
去括号得:9-3x≤6-2x+5,
移项、合并得:-x≤2,
系数化为1得:x≥-2,
解集表示在数轴上如图:
(4)去分母得:30+2(2-3x)≥5(x+1),
去括号得:30+4-6x≥5x+5,
移项、合并得:-11x≥-29,
系数化为1得:x≤$\frac{29}{11}$,
解集表示在数轴上如图:
点评 本题考查了解不等式的能力,解不等式要依据不等式的基本性质,在不等式的两边同时加上或减去同一个数或整式不等号的方向不变;在不等式的两边同时乘以或除以同一个正数不等号的方向不变;在不等式的两边同时乘以或除以同一个负数不等号的方向改变.在数轴上表示不等式的解集时,大于向右,小于向左,有等于号的画实心圆点,没有等于号的画空心圆圈.

练习册系列答案
相关题目
11.下列计算正确的是( )
| A. | x3•x5=x15 | B. | x4÷x=x3 | C. | 3x2•4x2=12x2 | D. | (x5)2=x7 |
6.一次函数y=kx+b中的x,y的部分对应值如下表:
根据表中数值分析以下四个结论:
①kb<0;
②y的值随x值的增大而减小;
③方程kx+b=-9的解是x=3;
④当x>-1时,y>7.
其中一定正确的是①②③④.
| x | … | -1 | 0 | 1 | 2 | … |
| y | … | 7 | 3 | -1 | -5 | … |
①kb<0;
②y的值随x值的增大而减小;
③方程kx+b=-9的解是x=3;
④当x>-1时,y>7.
其中一定正确的是①②③④.
7.长春市总面积为20565平方公里,20565这个数用科学记数法表示为( )
| A. | 20.565×102 | B. | 2.0565×103 | C. | 2.0565×104 | D. | 0.20565×104 |
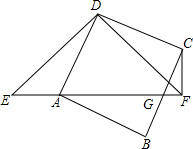 如图,已知在△EDF中,∠EDF=90°,DE=DF,A是EF上的点,以AD为边作正方形ABCD,它的边BC交EF于G点,连接FC.
如图,已知在△EDF中,∠EDF=90°,DE=DF,A是EF上的点,以AD为边作正方形ABCD,它的边BC交EF于G点,连接FC.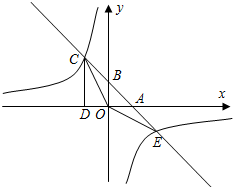 如图,已知一次函数y=k1x+b的图象分别x轴,y轴交于A、B两点,且与反比例函数y=$\frac{{k}_{2}}{x}$交于C、E两点,点C在第二象限,过点C作CD⊥x轴于点D,OD=1,OE=$\sqrt{10}$,cos∠AOE=$\frac{3\sqrt{10}}{10}$
如图,已知一次函数y=k1x+b的图象分别x轴,y轴交于A、B两点,且与反比例函数y=$\frac{{k}_{2}}{x}$交于C、E两点,点C在第二象限,过点C作CD⊥x轴于点D,OD=1,OE=$\sqrt{10}$,cos∠AOE=$\frac{3\sqrt{10}}{10}$ 已知四边形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,若P为AB边上任意一点,延长PD到E,使DE=2PD,再以PE,PC为边作平行四边形PCQE,则对角线PQ的长的最小值是6.
已知四边形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,若P为AB边上任意一点,延长PD到E,使DE=2PD,再以PE,PC为边作平行四边形PCQE,则对角线PQ的长的最小值是6.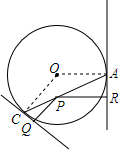 如图,设P为圆O内一定点,过P任作一弦AC,分别过A,C引圆的切线,再过P分别作两切线的垂线,垂足为Q,R.求证:$\frac{1}{PQ}$+$\frac{1}{PR}$为定值.
如图,设P为圆O内一定点,过P任作一弦AC,分别过A,C引圆的切线,再过P分别作两切线的垂线,垂足为Q,R.求证:$\frac{1}{PQ}$+$\frac{1}{PR}$为定值.