题目内容
4.已知直线y=kx经过第二、四象限,且$\sqrt{2k+3}$在实数范围内有意义,求k的取值范围.分析 根据y=kx经过第二、四象限,可得k<0,再由二次根式有意义的条件,即可得出k的取值范围.
解答 解:∵据y=kx经过第二、四象限,
∴k<0,
∵$\sqrt{2k+3}$在实数范围内有意义,
∴2k+3≥0,
∴k≥-$\frac{3}{2}$,
综上可得:-$\frac{3}{2}$≤k<0.
点评 本题考查了正比例函数的性质,注意二次根式有意义的条件:被开方数为非负数.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
16.若a<b,则下列各式中一定成立的是( )
| A. | ac<bc | B. | a2<b2 | C. | a+1<b+1 | D. | $\frac{a}{3}$>$\frac{b}{3}$ |
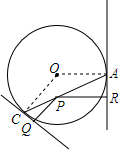 如图,设P为圆O内一定点,过P任作一弦AC,分别过A,C引圆的切线,再过P分别作两切线的垂线,垂足为Q,R.求证:$\frac{1}{PQ}$+$\frac{1}{PR}$为定值.
如图,设P为圆O内一定点,过P任作一弦AC,分别过A,C引圆的切线,再过P分别作两切线的垂线,垂足为Q,R.求证:$\frac{1}{PQ}$+$\frac{1}{PR}$为定值. 如图所示,?ABCD的周长为20cm,AE⊥BC于点E,AF⊥CD于点F,AE:AF=2:3,∠C=120°,则?ABCD的面积为24cm2.
如图所示,?ABCD的周长为20cm,AE⊥BC于点E,AF⊥CD于点F,AE:AF=2:3,∠C=120°,则?ABCD的面积为24cm2.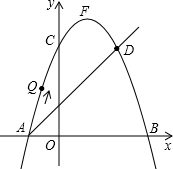 如图,在平面直角坐标系中,直线AD与抛物线y=-x2+bx+c交于A(-1,0)和D(2,3)两点,点C、F分别为该抛物线与y轴的交点和顶点.
如图,在平面直角坐标系中,直线AD与抛物线y=-x2+bx+c交于A(-1,0)和D(2,3)两点,点C、F分别为该抛物线与y轴的交点和顶点.