题目内容
4.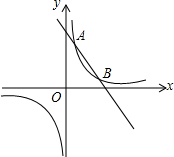 如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象相交于点A(2,5)和B,并且点A与点B关于第一、三象限的角平分线对称.
如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象相交于点A(2,5)和B,并且点A与点B关于第一、三象限的角平分线对称.(1)求这两个函数的表达式;
(2)观察图象,当x取何值时,y1>y2?
分析 (1)根据题意确定B的坐标,然后根据待定系数法即可求得;
(2)根据反比例函数与一次函数的交点A与B的横坐标,利用函数图象即可确定出所求x的范围.
解答 解:(1)∵一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象相交于点A(2,5)和B,
∴m=2×5=10,
∴反比例函数y2=$\frac{10}{x}$;
∵点A与点B关于第一、三象限的角平分线对称.
∴B(5,2),
把A、B代入得$\left\{\begin{array}{l}{2k+b=5}\\{5k+b=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-1}\\{b=7}\end{array}\right.$,
∴一次函数y1=-x+7;
(2)∵反比例函数与一次函数交点A(2,5)和B(5,2),
∴根据图象得:当y1>y2时,x的范围是x<0或2<x<5.
点评 此题考查了反比例函数与一次函数的交点问题,待定系数法求一次函数和反比例函数的解析式,利用了数形结合的思想,求得B的坐标是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 直线l1∥l2,一块含45°角的直角三角板如图所示放置,∠1=40°,则∠2=85°.
直线l1∥l2,一块含45°角的直角三角板如图所示放置,∠1=40°,则∠2=85°.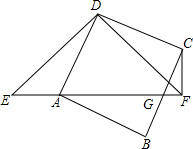 如图,已知在△EDF中,∠EDF=90°,DE=DF,A是EF上的点,以AD为边作正方形ABCD,它的边BC交EF于G点,连接FC.
如图,已知在△EDF中,∠EDF=90°,DE=DF,A是EF上的点,以AD为边作正方形ABCD,它的边BC交EF于G点,连接FC.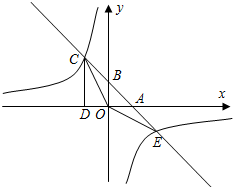 如图,已知一次函数y=k1x+b的图象分别x轴,y轴交于A、B两点,且与反比例函数y=$\frac{{k}_{2}}{x}$交于C、E两点,点C在第二象限,过点C作CD⊥x轴于点D,OD=1,OE=$\sqrt{10}$,cos∠AOE=$\frac{3\sqrt{10}}{10}$
如图,已知一次函数y=k1x+b的图象分别x轴,y轴交于A、B两点,且与反比例函数y=$\frac{{k}_{2}}{x}$交于C、E两点,点C在第二象限,过点C作CD⊥x轴于点D,OD=1,OE=$\sqrt{10}$,cos∠AOE=$\frac{3\sqrt{10}}{10}$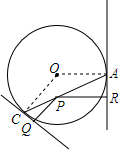 如图,设P为圆O内一定点,过P任作一弦AC,分别过A,C引圆的切线,再过P分别作两切线的垂线,垂足为Q,R.求证:$\frac{1}{PQ}$+$\frac{1}{PR}$为定值.
如图,设P为圆O内一定点,过P任作一弦AC,分别过A,C引圆的切线,再过P分别作两切线的垂线,垂足为Q,R.求证:$\frac{1}{PQ}$+$\frac{1}{PR}$为定值. 如图,在等腰直角三角形ABC中,∠ACB=90°,AB=4,以点A为圆心,AC长为半径作弧,交AB于点D,则图中阴影部分面积为4-π.
如图,在等腰直角三角形ABC中,∠ACB=90°,AB=4,以点A为圆心,AC长为半径作弧,交AB于点D,则图中阴影部分面积为4-π.