题目内容
3. 如图,点O是△ABC的内心,∠A=62°,则∠BOC=( )
如图,点O是△ABC的内心,∠A=62°,则∠BOC=( )| A. | 59° | B. | 31° | C. | 124° | D. | 121° |
分析 根据三角形内角和定理求出∠ACB+∠ABC,求出∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB),求出∠OBC+∠OCB的度数,根据三角形的内角和定理求出即可.
解答 解:∵∠BAC=62°,
∴∠ABC+∠ACB=180°-62°=118°,
∵点O是△ABC的内心,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×118°=59°,
∴∠BOC=180°-59°=121°.
故选D.
点评 本题考查了三角形的内角和定理,三角形的内切圆与内心的应用,关键是求出∠OBC+∠OCB的度数,题目比较典型,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13. 如图,正方形OABC的边长为6,A,C分别位于x轴、y轴上,点P在AB上,CP交OB于点Q,函数y=$\frac{k}{x}$的图象经过点Q,若S△BPQ=$\frac{1}{4}$S△OQC,则k的值为( )
如图,正方形OABC的边长为6,A,C分别位于x轴、y轴上,点P在AB上,CP交OB于点Q,函数y=$\frac{k}{x}$的图象经过点Q,若S△BPQ=$\frac{1}{4}$S△OQC,则k的值为( )
 如图,正方形OABC的边长为6,A,C分别位于x轴、y轴上,点P在AB上,CP交OB于点Q,函数y=$\frac{k}{x}$的图象经过点Q,若S△BPQ=$\frac{1}{4}$S△OQC,则k的值为( )
如图,正方形OABC的边长为6,A,C分别位于x轴、y轴上,点P在AB上,CP交OB于点Q,函数y=$\frac{k}{x}$的图象经过点Q,若S△BPQ=$\frac{1}{4}$S△OQC,则k的值为( )| A. | -12 | B. | 12 | C. | 16 | D. | 18 |
11.下列计算正确的是( )
| A. | x3•x5=x15 | B. | x4÷x=x3 | C. | 3x2•4x2=12x2 | D. | (x5)2=x7 |

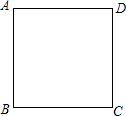 如图,四边形ABCD为正方形.在边AD上取一点E,连接BE,使∠AEB=60°.
如图,四边形ABCD为正方形.在边AD上取一点E,连接BE,使∠AEB=60°. 直线l1∥l2,一块含45°角的直角三角板如图所示放置,∠1=40°,则∠2=85°.
直线l1∥l2,一块含45°角的直角三角板如图所示放置,∠1=40°,则∠2=85°.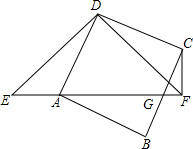 如图,已知在△EDF中,∠EDF=90°,DE=DF,A是EF上的点,以AD为边作正方形ABCD,它的边BC交EF于G点,连接FC.
如图,已知在△EDF中,∠EDF=90°,DE=DF,A是EF上的点,以AD为边作正方形ABCD,它的边BC交EF于G点,连接FC.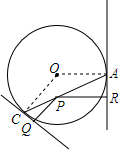 如图,设P为圆O内一定点,过P任作一弦AC,分别过A,C引圆的切线,再过P分别作两切线的垂线,垂足为Q,R.求证:$\frac{1}{PQ}$+$\frac{1}{PR}$为定值.
如图,设P为圆O内一定点,过P任作一弦AC,分别过A,C引圆的切线,再过P分别作两切线的垂线,垂足为Q,R.求证:$\frac{1}{PQ}$+$\frac{1}{PR}$为定值.