题目内容
1. 如图,已知长方形ABCD的两边长为AB=6,BC=4,将矩形ABCD绕着点C顺时针旋转90°后,点A转到点A′的位置上,对角线AC扫过的面积是13π.
如图,已知长方形ABCD的两边长为AB=6,BC=4,将矩形ABCD绕着点C顺时针旋转90°后,点A转到点A′的位置上,对角线AC扫过的面积是13π.
分析 根据长方形ABCD的两边长为AB=6,BC=4,可以求得对角戏AC的长,由矩形ABCD绕着点C顺时针旋转90°后,可知对角线AC扫过的面积正好是一个扇形,圆心角是90°,半径是AC的长,然后根据扇形的面积计算公式即可解答本题.
解答 解:由已知可得,
AB=6,BC=4,∠ABC=90°,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}=\sqrt{{6}^{2}+{4}^{2}}=\sqrt{52}=2\sqrt{13}$,
∵矩形ABCD绕着点C顺时针旋转90°
∴对角线AC扫过的面积是:$\frac{90×π×(2\sqrt{13})^{2}}{360}=13π$,
故答案为:13π.
点评 本题考查扇形面积的计算,解题的关键是明确扇形面积的计算公式,利用转化的数学思想进行解答.

练习册系列答案
相关题目
16.若a<b,则下列各式中一定成立的是( )
| A. | ac<bc | B. | a2<b2 | C. | a+1<b+1 | D. | $\frac{a}{3}$>$\frac{b}{3}$ |
6.一次函数y=kx+b中的x,y的部分对应值如下表:
根据表中数值分析以下四个结论:
①kb<0;
②y的值随x值的增大而减小;
③方程kx+b=-9的解是x=3;
④当x>-1时,y>7.
其中一定正确的是①②③④.
| x | … | -1 | 0 | 1 | 2 | … |
| y | … | 7 | 3 | -1 | -5 | … |
①kb<0;
②y的值随x值的增大而减小;
③方程kx+b=-9的解是x=3;
④当x>-1时,y>7.
其中一定正确的是①②③④.
11.如果∠1与∠2的两边互相平行,那么这两个角( )
| A. | 相等 | B. | 互补 | C. | 相等或互补 | D. | 无法确定 |
 直线l1∥l2,一块含45°角的直角三角板如图所示放置,∠1=40°,则∠2=85°.
直线l1∥l2,一块含45°角的直角三角板如图所示放置,∠1=40°,则∠2=85°.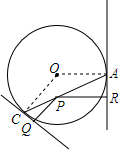 如图,设P为圆O内一定点,过P任作一弦AC,分别过A,C引圆的切线,再过P分别作两切线的垂线,垂足为Q,R.求证:$\frac{1}{PQ}$+$\frac{1}{PR}$为定值.
如图,设P为圆O内一定点,过P任作一弦AC,分别过A,C引圆的切线,再过P分别作两切线的垂线,垂足为Q,R.求证:$\frac{1}{PQ}$+$\frac{1}{PR}$为定值. 如图所示,?ABCD的周长为20cm,AE⊥BC于点E,AF⊥CD于点F,AE:AF=2:3,∠C=120°,则?ABCD的面积为24cm2.
如图所示,?ABCD的周长为20cm,AE⊥BC于点E,AF⊥CD于点F,AE:AF=2:3,∠C=120°,则?ABCD的面积为24cm2. 如图,在等腰直角三角形ABC中,∠ACB=90°,AB=4,以点A为圆心,AC长为半径作弧,交AB于点D,则图中阴影部分面积为4-π.
如图,在等腰直角三角形ABC中,∠ACB=90°,AB=4,以点A为圆心,AC长为半径作弧,交AB于点D,则图中阴影部分面积为4-π.