题目内容
16.为调查某校学生一学期课外书的阅读量情况,从全校学生中随机抽取50名学生的阅读情况进行分析,并规定如下:设一个学生一学期阅读课外书籍本数为n,当0≤n<5时,该学生为一般读者;当5≤n<10时,该学生为良好读者;当n≥10时,该学生为优秀读者.随机抽取的50名学生一学期阅读课外书的本数数据如下:
| 阅读本数n | 0 | 2 | 4 | 5 | 6 | 8 | 10 | 12 | 14 | 16 |
| 人数 | 1 | 1 | 2 | 3 | 12 | 11 | 5 | 8 | 5 | 2 |
(1)请你估计在全校学生中任意抽取一个学生,是良好读者的概率是多少?(直接写出结果)
(2)在样本中为一般读者的学生中随机抽取2人,用树状图或列表法求抽得2人的课外书籍阅读本数都为4本的概率.
分析 (1)由给出的数据可求出当5≤n<10时的人数,进而可求得良好读者的概率;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与抽得2人的课外书籍阅读本数都为4的情况,再利用概率公式即可求得答案.
解答 解:
(1)∵5≤n<10时,学生的人数为3+12+11=26(人),
∴估计在全校学生中任意抽取一个学生,是良好读者的概率=$\frac{26}{50}$=$\frac{13}{25}$;
(2)画树状图得:
∵共有12种等可能的结果,抽得2人的课外书籍阅读本数都为4的有2种情况,
∴抽得2人的课外书籍阅读本数都为4的概率为:$\frac{2}{12}$=$\frac{1}{6}$.
点评 本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
4. 如图,直线l1与l2相交,且夹角为60°,点P在角的内部,小明用下面的方法作P的对称点:先以l1为对称轴作点P关于l1的对称点P1,再以l2为对称轴作P1关于l2的对称点P2,然后再以l1为对称轴作P2关于l1的对称点P3,以l2为对称轴作P3关于l2的对称点P4,…,如此继续,得到一系列的点P1,P2,…,Pn,若Pn与P重合,则n的可以是( )
如图,直线l1与l2相交,且夹角为60°,点P在角的内部,小明用下面的方法作P的对称点:先以l1为对称轴作点P关于l1的对称点P1,再以l2为对称轴作P1关于l2的对称点P2,然后再以l1为对称轴作P2关于l1的对称点P3,以l2为对称轴作P3关于l2的对称点P4,…,如此继续,得到一系列的点P1,P2,…,Pn,若Pn与P重合,则n的可以是( )
 如图,直线l1与l2相交,且夹角为60°,点P在角的内部,小明用下面的方法作P的对称点:先以l1为对称轴作点P关于l1的对称点P1,再以l2为对称轴作P1关于l2的对称点P2,然后再以l1为对称轴作P2关于l1的对称点P3,以l2为对称轴作P3关于l2的对称点P4,…,如此继续,得到一系列的点P1,P2,…,Pn,若Pn与P重合,则n的可以是( )
如图,直线l1与l2相交,且夹角为60°,点P在角的内部,小明用下面的方法作P的对称点:先以l1为对称轴作点P关于l1的对称点P1,再以l2为对称轴作P1关于l2的对称点P2,然后再以l1为对称轴作P2关于l1的对称点P3,以l2为对称轴作P3关于l2的对称点P4,…,如此继续,得到一系列的点P1,P2,…,Pn,若Pn与P重合,则n的可以是( )| A. | 2016 | B. | 2015 | C. | 2014 | D. | 2012 |
5.下列说法正确的有( )
①有两边和一角对应相等的两个三角形全等;
②有一个角为100°,且腰长对应相等的两个等腰三角形全等;
③有两边及第三边上的高对应相等的两个三角形全等;
④三条边对应相等的两个三角形对应角也是相等的.
①有两边和一角对应相等的两个三角形全等;
②有一个角为100°,且腰长对应相等的两个等腰三角形全等;
③有两边及第三边上的高对应相等的两个三角形全等;
④三条边对应相等的两个三角形对应角也是相等的.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.下列四个数中,其相反数是正整数的是( )
| A. | 2 | B. | $\frac{5}{13}$ | C. | -2016 | D. | -$\frac{2}{3}$ |
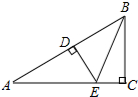 如图:∠C=90°,DE⊥AB,垂足为D,BC=BD,若AC=3cm,则AE+DE=3cm.
如图:∠C=90°,DE⊥AB,垂足为D,BC=BD,若AC=3cm,则AE+DE=3cm. 如图,在Rt△OAB中,∠OAB=90°,点B的坐标为(4,2).
如图,在Rt△OAB中,∠OAB=90°,点B的坐标为(4,2).
