题目内容
7．
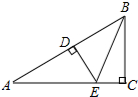如图：∠C=90°，DE⊥AB，垂足为D，BC=BD，若AC=3cm，则AE+DE=3cm．
分析 根据∠C=90°，DE⊥AB，又有BC=BD，BE=BE，得出△BDE≌△BCE，可得DE=CE，然后有AE+DE=AE+EC=AC=3cm，即可得解．
解答 解：∵∠C=90°，DE⊥AB，
则在Rt△△BDE和Rt△BCE中，
∵$\left\{\begin{array}{l}{BE=BE}\\{BD=BC}\end{array}\right.$，
∴△BDE≌△BCE（HL），
∴DE=CE，
∴AE+DE=AE+EC=AC=3cm．
故答案为：3cm．
点评 本题考查了全等三角形的判定与性质，解答本题的关键是根据题目中的条件利用HL判定△BDE≌△BCE，难度适中．
练习册系列答案
相关题目
15．下列代数式中，符合书写格式的是（ ）
| A． | $\frac{{a}^{2}b}{4}$ | B． | 2$\frac{1}{3}$ab | C． | a×b÷2 | D． | a×2 |
如图：△ABC中，AD为∠BAC的角平分线，EF垂直平分AD，E为垂足，EF交BC的延长线于点F，求证：∠B=∠CAF．
如图，在Rt△ABC中，∠C=90°，点E在斜边AB上，以AE为直径的⊙O与BC相切于点D，若BE=6，BD=6．
已知抛物线的解析式为：y=x2-4x+3在平面直角坐标系中画出这条抛物线．
16．为调查某校学生一学期课外书的阅读量情况，从全校学生中随机抽取50名学生的阅读情况进行分析，并规定如下：设一个学生一学期阅读课外书籍本数为n，当0≤n＜5时，该学生为一般读者；当5≤n＜10时，该学生为良好读者；当n≥10时，该学生为优秀读者．
随机抽取的50名学生一学期阅读课外书的本数数据如下：
根据以上数据回答下列问题：
（1）请你估计在全校学生中任意抽取一个学生，是良好读者的概率是多少？（直接写出结果）
（2）在样本中为一般读者的学生中随机抽取2人，用树状图或列表法求抽得2人的课外书籍阅读本数都为4本的概率．
随机抽取的50名学生一学期阅读课外书的本数数据如下：
| 阅读本数n | 0 | 2 | 4 | 5 | 6 | 8 | 10 | 12 | 14 | 16 |
| 人数 | 1 | 1 | 2 | 3 | 12 | 11 | 5 | 8 | 5 | 2 |
（1）请你估计在全校学生中任意抽取一个学生，是良好读者的概率是多少？（直接写出结果）
（2）在样本中为一般读者的学生中随机抽取2人，用树状图或列表法求抽得2人的课外书籍阅读本数都为4本的概率．
