题目内容
1．
如图，直线AB，CD相交于点O，EO⊥CD于点O，∠AOE=36°，则∠BOD=（ ）| A． | 36° | B． | 44° | C． | 50° | D． | 54° |
分析 根据题意可以得到∠EOD的度数，由∠AOE=36°，∠AOE+∠EOD+∠BOD=180°，从而可以得到∠BOD的度数．
解答 解：∵EO⊥CD，
∴∠EOD=90°，
又∵∠AOE+∠EOD+∠BOD=180°，∠AOE=36°，
∴∠BOD=54°，
故选D．
点评 本题考查垂线、平角，解题的关键是明确题意，找出所求问题需要的条件．
练习册系列答案
相关题目
11．已知点A（1，2）在反比例函数y=$\frac{k}{x}$的图象上，则该反比例函数的解析式是（ ）
| A． | y=$\frac{1}{x}$ | B． | y=$\frac{4}{x}$ | C． | y=$\frac{2}{x}$ | D． | y=2x |
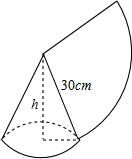如图，用一个半径为30cm，面积为300πcm2的扇形铁皮，制作一个无底的圆锥（不计损耗），则圆锥的高h等于20$\sqrt{2}$cm．
如图，直角三角形ABC中，∠ACB=90°，AB=10，BC=6，在线段AB上取一点D，作DF⊥AB交AC于点F，现将△ADF沿DF折叠，使点A落在线段DB上，对应点记为H，AD的中点E的对应点记为G，若△GFH∽△GBF，则AD=$\frac{16}{5}$．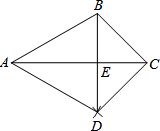
如图，已知△ABC，按如下步骤作图：
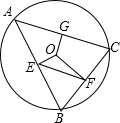如图，⊙O的半径是$\sqrt{5}$，△ABC是⊙O的内接三角形，过圆心O分别作AB，BC，AC的垂线，垂足为E，F，G，连接EF，若OG=1，则EF的长为2．