题目内容
10.点P为⊙O内一点,过点P的最长的弦长为10cm,最短的弦长为8cm,那么OP的长等于3cm.分析 根据直径是圆中最长的弦,知该圆的直径是10cm;最短弦即是过点P且垂直于过点P的直径的弦;根据垂径定理即可求得CP的长,再进一步根据勾股定理,可以求得OP的长.
解答 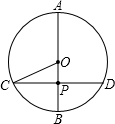 解:如图所示,CD⊥AB于点P.
解:如图所示,CD⊥AB于点P.
根据题意,得
AB=10cm,CD=8cm.
∵CD⊥AB,
∴CP=$\frac{1}{2}$CD=4cm.
根据勾股定理,得OP=$\sqrt{O{C}^{2}-C{P}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3(cm).
故答案为:3.
点评 此题综合运用了垂径定理和勾股定理.正确理解圆中,过一点的最长的弦和最短的弦.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1. 如图,直线AB,CD相交于点O,EO⊥CD于点O,∠AOE=36°,则∠BOD=( )
如图,直线AB,CD相交于点O,EO⊥CD于点O,∠AOE=36°,则∠BOD=( )
 如图,直线AB,CD相交于点O,EO⊥CD于点O,∠AOE=36°,则∠BOD=( )
如图,直线AB,CD相交于点O,EO⊥CD于点O,∠AOE=36°,则∠BOD=( )| A. | 36° | B. | 44° | C. | 50° | D. | 54° |
15.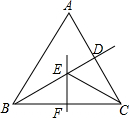 如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E,如果∠BAC=60°,∠ACE=24°,那么∠BCE的大小是( )
如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E,如果∠BAC=60°,∠ACE=24°,那么∠BCE的大小是( )
 如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E,如果∠BAC=60°,∠ACE=24°,那么∠BCE的大小是( )
如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E,如果∠BAC=60°,∠ACE=24°,那么∠BCE的大小是( )| A. | 24° | B. | 30° | C. | 32° | D. | 36° |

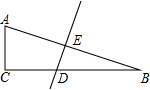 如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线分别交AB、BC于点E和点D,已知BD:CD=2:$\sqrt{3}$.
如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线分别交AB、BC于点E和点D,已知BD:CD=2:$\sqrt{3}$. 如图,点C到直线AB的距离是线段BC的长.
如图,点C到直线AB的距离是线段BC的长.