题目内容
13.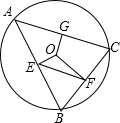 如图,⊙O的半径是$\sqrt{5}$,△ABC是⊙O的内接三角形,过圆心O分别作AB,BC,AC的垂线,垂足为E,F,G,连接EF,若OG=1,则EF的长为2.
如图,⊙O的半径是$\sqrt{5}$,△ABC是⊙O的内接三角形,过圆心O分别作AB,BC,AC的垂线,垂足为E,F,G,连接EF,若OG=1,则EF的长为2.
分析 连接OA,根据勾股定理求出AG,根据垂径定理求出AC,根据垂径定理得到EF是△ABC的中位线,根据中位线定理计算即可.
解答 解: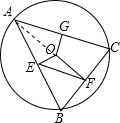 连接OA,
连接OA,
∵OG⊥AC,OA=$\sqrt{5}$,OG=1,
∴AG=$\sqrt{O{A}^{2}-O{G}^{2}}$=2,
∵OG⊥AC,
∴AC=2AG=4,
∵OE⊥AB,OF⊥BC,
∴AE=EB,BF=FC,
∴EF=$\frac{1}{2}$AC=2.
故答案为:2.
点评 本题考查的是三角形中位线定理、垂径定理和勾股定理的应用,三角形的中位线平行于第三边,并且等于第三边的一半,垂直弦的直径平分这条弦,并且平分弦所对的两条弧.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
1. 如图,直线AB,CD相交于点O,EO⊥CD于点O,∠AOE=36°,则∠BOD=( )
如图,直线AB,CD相交于点O,EO⊥CD于点O,∠AOE=36°,则∠BOD=( )
 如图,直线AB,CD相交于点O,EO⊥CD于点O,∠AOE=36°,则∠BOD=( )
如图,直线AB,CD相交于点O,EO⊥CD于点O,∠AOE=36°,则∠BOD=( )| A. | 36° | B. | 44° | C. | 50° | D. | 54° |
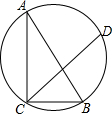 如图,一块含30°角的直角三角形ABC的三个顶点刚好都在一个圆上,已知弦CD与CB的夹角∠BCD=40°,BC=3,则$\widehat{BD}$的长度为$\frac{4π}{3}$(结果保留π).
如图,一块含30°角的直角三角形ABC的三个顶点刚好都在一个圆上,已知弦CD与CB的夹角∠BCD=40°,BC=3,则$\widehat{BD}$的长度为$\frac{4π}{3}$(结果保留π).
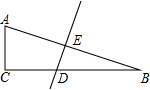 如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线分别交AB、BC于点E和点D,已知BD:CD=2:$\sqrt{3}$.
如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线分别交AB、BC于点E和点D,已知BD:CD=2:$\sqrt{3}$.