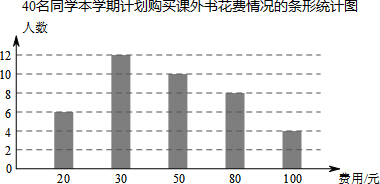
题目内容
12.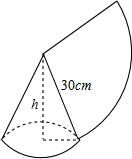 如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的高h等于20$\sqrt{2}$cm.
如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的高h等于20$\sqrt{2}$cm.
分析 由圆锥的几何特征,我们可得用半径为30cm,面积为300πcm2的扇形铁皮制作一个无盖的圆锥形容器,则圆锥的底面周长等于扇形的弧长,据此求得圆锥的底面圆的半径,利用勾股定理求得高即可.
解答 解:设铁皮扇形的半径和弧长分别为R、l,圆锥形容器底面半径为r,
则由题意得R=30,由$\frac{1}{2}$Rl=300π得l=20π;
由2πr=l得r=10cm.
h=$\sqrt{3{0}^{2}-1{0}^{2}}$=20$\sqrt{2}$cm,
故答案是:20$\sqrt{2}$cm.
点评 本题考查的知识点是圆锥的表面积,其中根据已知制作一个无盖的圆锥形容器的扇形铁皮的相关几何量,计算出圆锥的底面半径和高,是解答本题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
7.已知一组数据:1,3,2,6,3.下列关于这组数据的说法,不正确的是( )
| A. | 方差是1.8 | B. | 众数是3 | C. | 中位数是3 | D. | 平均数是3 |
17.下列计算中,正确的是( )
| A. | a3+a3=a6 | B. | a3•a2=a6 | C. | (-a3)2=a9 | D. | (-a2)3=-a6 |
1. 如图,直线AB,CD相交于点O,EO⊥CD于点O,∠AOE=36°,则∠BOD=( )
如图,直线AB,CD相交于点O,EO⊥CD于点O,∠AOE=36°,则∠BOD=( )
 如图,直线AB,CD相交于点O,EO⊥CD于点O,∠AOE=36°,则∠BOD=( )
如图,直线AB,CD相交于点O,EO⊥CD于点O,∠AOE=36°,则∠BOD=( )| A. | 36° | B. | 44° | C. | 50° | D. | 54° |
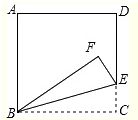 如图,将正方形纸片ABCD沿BE翻折,使点C落在点F处,若∠DEF=40°,则∠ABF的度数为50°.
如图,将正方形纸片ABCD沿BE翻折,使点C落在点F处,若∠DEF=40°,则∠ABF的度数为50°.