题目内容
下列分式的值,可以为零的是( )
A. 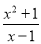 B.
B. 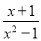 C.
C. 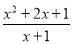 D.
D. 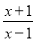
 C
【解析】A. ∵x2+1>0, ∴≠0;
B. ∵x+1=0时,x=1,此时分母x2-1=0, ∴≠0;
C. ∵x2+2x+1=0时,x=-1,此时分母x+1=0, ∴ ≠0;
D. ∵x+1=0时,x=-1,此时分母x-1≠0, ∴当x=-1时, =0.
故选D.
C
【解析】A. ∵x2+1>0, ∴≠0;
B. ∵x+1=0时,x=1,此时分母x2-1=0, ∴≠0;
C. ∵x2+2x+1=0时,x=-1,此时分母x+1=0, ∴ ≠0;
D. ∵x+1=0时,x=-1,此时分母x-1≠0, ∴当x=-1时, =0.
故选D.
练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
已知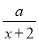 与
与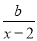 的和等于
的和等于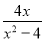 ,求
,求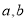 之值.
之值.
 a=2,b=2
【解析】【试题分析】根据题意得: 变形 ,得: 得: ,从而得解.
【试题解析】
根据题意,有
+=.
去分母,得
.
去括号,整理得
.
比较两边多项式系数,得
.
解得.
a=2,b=2
【解析】【试题分析】根据题意得: 变形 ,得: 得: ,从而得解.
【试题解析】
根据题意,有
+=.
去分母,得
.
去括号,整理得
.
比较两边多项式系数,得
.
解得. 若 ,则
,则 =____________.
=____________.
 5
【解析】试题解析:
把代入,得
故答案为:
5
【解析】试题解析:
把代入,得
故答案为: 计算:
(1) (2)
(2) ÷(4x2﹣y2)
÷(4x2﹣y2)
 (1) ;(2)
【解析】试题分析:(1)考查了分式的乘除混合运算,从左到右依次计算即可;(2)先把除法转化为乘法,然后把分子和分母分解因式约分.
【解析】
(1)原式=×
=;
(2)原式=•
=(2x﹣y)•
=;
(1) ;(2)
【解析】试题分析:(1)考查了分式的乘除混合运算,从左到右依次计算即可;(2)先把除法转化为乘法,然后把分子和分母分解因式约分.
【解析】
(1)原式=×
=;
(2)原式=•
=(2x﹣y)•
=; 对于分式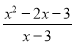 ,当x=__时,分式无意义;当x=__时,分式值为零.
,当x=__时,分式无意义;当x=__时,分式值为零.
 3, -1
【解析】当x-3=0时,分式无意义,
解之得
x=3;
当 时,分式值为零,
解之得
x=-1.
3, -1
【解析】当x-3=0时,分式无意义,
解之得
x=3;
当 时,分式值为零,
解之得
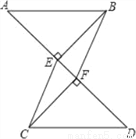
x=-1. 如图,已知AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF. 求证:四边形BECF是平行四边形.
 见解析
【解析】试题分析:通过全等三角形(△AEB≌△DFC)的对应边相等证得BE=CF,由“在同一平面内,同垂直于同一条直线的两条直线相互平行”证得BE∥CF.则四边形BECF是平行四边形.
证明:∵BE⊥AD,CF⊥AD,
∴∠AEB=∠DFC=90°,
∵AB∥CD,
∴∠A=∠D,
在△AEB与△DFC中,
,
∴△AEB≌△DFC(ASA)...
见解析
【解析】试题分析:通过全等三角形(△AEB≌△DFC)的对应边相等证得BE=CF,由“在同一平面内,同垂直于同一条直线的两条直线相互平行”证得BE∥CF.则四边形BECF是平行四边形.
证明:∵BE⊥AD,CF⊥AD,
∴∠AEB=∠DFC=90°,
∵AB∥CD,
∴∠A=∠D,
在△AEB与△DFC中,
,
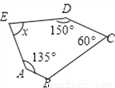
∴△AEB≌△DFC(ASA)... 如图,已知AB∥CD,则x的度数是____________.
 75º
【解析】∵AB∥CD,
∴∠B=180°-60°=120°,
∵多边形ABCDE是五边形,
∴∠A+∠B+∠C+∠D+∠E=(5-2)×180°=540°,
∴∠E=540°-∠A-∠B-∠C-∠D=540°-135°-120°-60°-150°=75°.
75º
【解析】∵AB∥CD,
∴∠B=180°-60°=120°,
∵多边形ABCDE是五边形,
∴∠A+∠B+∠C+∠D+∠E=(5-2)×180°=540°,
∴∠E=540°-∠A-∠B-∠C-∠D=540°-135°-120°-60°-150°=75°. 解方程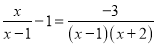
 【解析】分析:观察可得最简公分母是(x-1)(x+2),方程两边乘最简公分母,可以把分式方程转化为整式方程求解;
本题解析:两边同时乘最简公分母
化成整式方程为:
整理得到: ,经检验是方程的解.
【解析】分析:观察可得最简公分母是(x-1)(x+2),方程两边乘最简公分母,可以把分式方程转化为整式方程求解;
本题解析:两边同时乘最简公分母
化成整式方程为:
整理得到: ,经检验是方程的解. 化简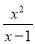 +
+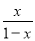 的结果是__;当x=2时,原式的值为__.
的结果是__;当x=2时,原式的值为__.
 x 2
【解析】试题解析:
原式
当时,原式
故答案为:
x 2
【解析】试题解析:
原式
当时,原式
故答案为: 
