题目内容
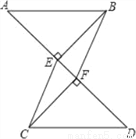
如图,已知AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF. 求证:四边形BECF是平行四边形.
 见解析
【解析】试题分析:通过全等三角形(△AEB≌△DFC)的对应边相等证得BE=CF,由“在同一平面内,同垂直于同一条直线的两条直线相互平行”证得BE∥CF.则四边形BECF是平行四边形.
证明:∵BE⊥AD,CF⊥AD,
∴∠AEB=∠DFC=90°,
∵AB∥CD,
∴∠A=∠D,
在△AEB与△DFC中,
,
∴△AEB≌△DFC(ASA)...
见解析
【解析】试题分析:通过全等三角形(△AEB≌△DFC)的对应边相等证得BE=CF,由“在同一平面内,同垂直于同一条直线的两条直线相互平行”证得BE∥CF.则四边形BECF是平行四边形.
证明:∵BE⊥AD,CF⊥AD,
∴∠AEB=∠DFC=90°,
∵AB∥CD,
∴∠A=∠D,
在△AEB与△DFC中,
,
∴△AEB≌△DFC(ASA)...
练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
若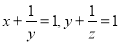 ,则
,则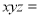 _____.
_____.
 -1
【解析】根据得: .
故答案:-1.
-1
【解析】根据得: .
故答案:-1. 已知 ,则M等于( )
,则M等于( )
A.  B.
B.  C.
C.  D.
D. 
 A
【解析】试题解析:试题解析:
故选A.
A
【解析】试题解析:试题解析:
故选A. 下列各式① ;②
;②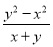 ;③
;③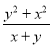 ;④
;④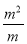 ;⑤
;⑤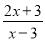 中分子与分母没有公因式的分式是__.(填序号)
中分子与分母没有公因式的分式是__.(填序号)
 ③⑤
【解析】①∵=, ∴分子与分母有公因式3;
②∵∴分子与分母有公因式x+y;
③的分子与分母没有公因式;
④∵∴分子与分母有公因式m;
⑤的分子与分母没有公因式.
∴③和⑤的分子与分母没有公因式.
③⑤
【解析】①∵=, ∴分子与分母有公因式3;
②∵∴分子与分母有公因式x+y;
③的分子与分母没有公因式;
④∵∴分子与分母有公因式m;
⑤的分子与分母没有公因式.
∴③和⑤的分子与分母没有公因式. 下列分式的值,可以为零的是( )
A. 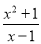 B.
B. 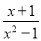 C.
C. 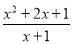 D.
D. 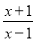
 C
【解析】A. ∵x2+1>0, ∴≠0;
B. ∵x+1=0时,x=1,此时分母x2-1=0, ∴≠0;
C. ∵x2+2x+1=0时,x=-1,此时分母x+1=0, ∴ ≠0;
D. ∵x+1=0时,x=-1,此时分母x-1≠0, ∴当x=-1时, =0.
故选D.
C
【解析】A. ∵x2+1>0, ∴≠0;
B. ∵x+1=0时,x=1,此时分母x2-1=0, ∴≠0;
C. ∵x2+2x+1=0时,x=-1,此时分母x+1=0, ∴ ≠0;
D. ∵x+1=0时,x=-1,此时分母x-1≠0, ∴当x=-1时, =0.
故选D. 如图所示,在□ABCD中,AC与BD相交于点O,AB⊥AC,∠DAC=45°,AC=2,则BD的长是_______.

 2
【解析】∵四边形ABCD是平行四边形,∠DAC=45°,
∴∠ACB=∠DAC=45°,OA=AC=1,
∵AB⊥AC,
∴△ABC是等腰直角三角形,
∴AB=AC=2,
在Rt△AOB中,根据勾股定理得OB= ,
∴BD=2BO=2.
2
【解析】∵四边形ABCD是平行四边形,∠DAC=45°,
∴∠ACB=∠DAC=45°,OA=AC=1,
∵AB⊥AC,
∴△ABC是等腰直角三角形,
∴AB=AC=2,
在Rt△AOB中,根据勾股定理得OB= ,
∴BD=2BO=2. 如图,四边形ABCD是平行四边形,点E在边BC上,如果点F是边AD上的点,那么△CDF与△ABE不一定全等的条件是( )
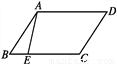
A. DF=BE B. AF=CE
C. CF=AE D. CF∥AE
 C
【解析】试题分析:A、当DF=BE时,有平行四边形的性质可得:AB=CD,∠B=∠D,利用SAS可判定△CDF≌△ABE;B、当AF=CE时,有平行四边形的性质可得:BE=DF,AB=CD,∠B=∠D,利用SAS可判定△CDF≌△ABE;C、当CF=AE时,有平行四边形的性质可得:AB=CD,∠B=∠D,利用SSA不能判定△CDF≌△ABE;D、当CF∥AE时,有平行四边形的性质可得:A...
C
【解析】试题分析:A、当DF=BE时,有平行四边形的性质可得:AB=CD,∠B=∠D,利用SAS可判定△CDF≌△ABE;B、当AF=CE时,有平行四边形的性质可得:BE=DF,AB=CD,∠B=∠D,利用SAS可判定△CDF≌△ABE;C、当CF=AE时,有平行四边形的性质可得:AB=CD,∠B=∠D,利用SSA不能判定△CDF≌△ABE;D、当CF∥AE时,有平行四边形的性质可得:A... 分式方程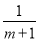 =
=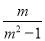 的最简公分母是__________
的最简公分母是__________
 【解析】式子,所以最简公分母是.故答案为: .
【解析】式子,所以最简公分母是.故答案为: . 下列各式计算正确的是( )
A. 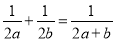 B.
B.  C.
C.  D.
D. 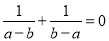
 D
【解析】试题解析:A.原式故A错误;
B.原式故B错误;
C.原式故C错误;
D.正确.
故选D.
D
【解析】试题解析:A.原式故A错误;
B.原式故B错误;
C.原式故C错误;
D.正确.
故选D. 
