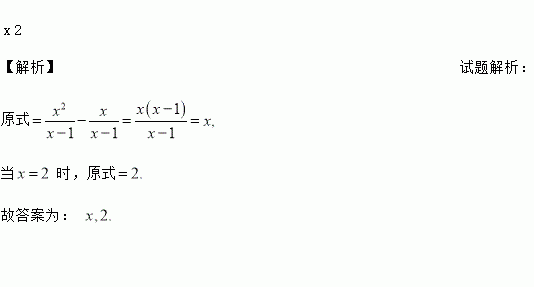题目内容
化简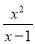 +
+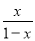 的结果是__;当x=2时,原式的值为__.
的结果是__;当x=2时,原式的值为__.
 x 2
【解析】试题解析:
原式
当时,原式
故答案为:
x 2
【解析】试题解析:
原式
当时,原式
故答案为:
练习册系列答案
相关题目
下列分式的值,可以为零的是( )
A. 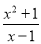 B.
B. 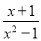 C.
C. 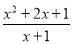 D.
D. 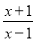
 C
【解析】A. ∵x2+1>0, ∴≠0;
B. ∵x+1=0时,x=1,此时分母x2-1=0, ∴≠0;
C. ∵x2+2x+1=0时,x=-1,此时分母x+1=0, ∴ ≠0;
D. ∵x+1=0时,x=-1,此时分母x-1≠0, ∴当x=-1时, =0.
故选D.
C
【解析】A. ∵x2+1>0, ∴≠0;
B. ∵x+1=0时,x=1,此时分母x2-1=0, ∴≠0;
C. ∵x2+2x+1=0时,x=-1,此时分母x+1=0, ∴ ≠0;
D. ∵x+1=0时,x=-1,此时分母x-1≠0, ∴当x=-1时, =0.
故选D. 下列各式变形正确的是( )
A. 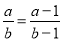 B.
B. 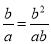 C.
C. 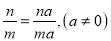 D.
D. 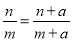
 C
【解析】A项,在原分式的分子分母上加上一个整式,等式不一定成立。故A项错误。
B项,由于b的值可能为0。故B项错误。
C项, )成立。故C项正确。
D项,在原分式的分子分母上加上一个整式,等式不一定成立。故D项错误。故本题正确答案为C。
C
【解析】A项,在原分式的分子分母上加上一个整式,等式不一定成立。故A项错误。
B项,由于b的值可能为0。故B项错误。
C项, )成立。故C项正确。
D项,在原分式的分子分母上加上一个整式,等式不一定成立。故D项错误。故本题正确答案为C。 化简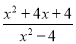 -
-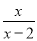 =______.
=______.
 【解析】-
=-
=-
=
【解析】-
=-
=-
= 计算: 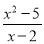 -
-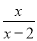 -
-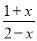
 x+2
【解析】试题分析:根据分式加减的运算法则进行运算即可.
试题解析:原式
x+2
【解析】试题分析:根据分式加减的运算法则进行运算即可.
试题解析:原式 下列各式计算正确的是( )
A. 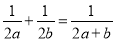 B.
B.  C.
C.  D.
D. 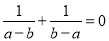
 D
【解析】试题解析:A.原式故A错误;
B.原式故B错误;
C.原式故C错误;
D.正确.
故选D.
D
【解析】试题解析:A.原式故A错误;
B.原式故B错误;
C.原式故C错误;
D.正确.
故选D. 在△ABC中,AB=AC,AD是BC边上的高,∠C=63°,BC=4,求∠BAD的度数及DC的长.
 27° 2
【解析】试题分析:根据等腰三角形的两个底角相等求出顶角∠BAC的度数,再由等腰三角形的三线合一性质即可求出∠BAD=∠BAC=27°,DC=BC=2.
试题解析:
∵AB=AC,∠C=63°,
∴∠B=∠C=63°,
∴∠BAC=180°-63°-63°=54°.
又∵AD是BC边上的高,
∴AD是∠BAC的平分线,AD是BC边上的中线,
...
27° 2
【解析】试题分析:根据等腰三角形的两个底角相等求出顶角∠BAC的度数,再由等腰三角形的三线合一性质即可求出∠BAD=∠BAC=27°,DC=BC=2.
试题解析:
∵AB=AC,∠C=63°,
∴∠B=∠C=63°,
∴∠BAC=180°-63°-63°=54°.
又∵AD是BC边上的高,
∴AD是∠BAC的平分线,AD是BC边上的中线,
... 等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为( )
A. 60° B. 120° C. 60°或150° D. 60°或120°
 D
【解析】试题分析:等腰三角形的高相对于三角形有三种位置关系,三角形内部,三角形的外部,三角形的边上.根据条件可知第三种高在三角形的边上这种情况不成了,因而应分两种情况进行讨论.
【解析】
当高在三角形内部时(如图1),顶角是60°;
当高在三角形外部时(如图2),顶角是120°.
故选D.
D
【解析】试题分析:等腰三角形的高相对于三角形有三种位置关系,三角形内部,三角形的外部,三角形的边上.根据条件可知第三种高在三角形的边上这种情况不成了,因而应分两种情况进行讨论.
【解析】
当高在三角形内部时(如图1),顶角是60°;
当高在三角形外部时(如图2),顶角是120°.
故选D. (3a-b)(3a+b)-(a+b)2
 8a2-2b2-2ab
【解析】试题分析:先根据平方差公式与完全平方公式分别计算,再合并同类项即可.
试题解析:
(3a-b)(3a+b)-(a+b)2=9a2-b2-a2-b2-2ab=8a2-2b2-2ab.
8a2-2b2-2ab
【解析】试题分析:先根据平方差公式与完全平方公式分别计算,再合并同类项即可.
试题解析:
(3a-b)(3a+b)-(a+b)2=9a2-b2-a2-b2-2ab=8a2-2b2-2ab.