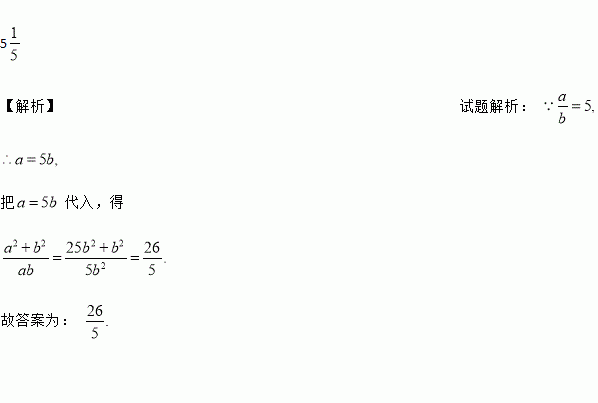题目内容
若 ,则
,则 =____________.
=____________.
 5
【解析】试题解析:
把代入,得
故答案为:
5
【解析】试题解析:
把代入,得
故答案为:
练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
平行四边形ABCD的周长32,5AB=3BC,则对角线AC的取值范围为( )
A.6<AC<10 B.6<AC<16 C.10<AC<16 D.4<AC<16
 D.
【解析】
试题分析:∵平行四边形ABCD的周长32,5AB=3BC,∴2(AB+BC)=2(BC+BC)=32,
∴BC=10,∴AB=6,∴BC﹣AB<AC<BC+AB,即4<AC<16.
故选D.
D.
【解析】
试题分析:∵平行四边形ABCD的周长32,5AB=3BC,∴2(AB+BC)=2(BC+BC)=32,
∴BC=10,∴AB=6,∴BC﹣AB<AC<BC+AB,即4<AC<16.
故选D. 已知x=2时,分式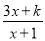 的值为零,则k=__________.
的值为零,则k=__________.
 -6
【解析】由题意得:6+k=0,解得:k=-6.
故答案:-6.
-6
【解析】由题意得:6+k=0,解得:k=-6.
故答案:-6. 有三个连续正整数,其倒数之和是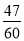 ,那么这三个数中最小的是( )
,那么这三个数中最小的是( )
A. 1 B. 2 C. 3 D. 4
 C
【解析】设三个连续正整数分别为: ,根据题意得:
解得: 则 .
故选C.
C
【解析】设三个连续正整数分别为: ,根据题意得:
解得: 则 .
故选C. 计算:
(1)(xy-x2)÷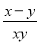 (2)
(2) 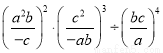
(3)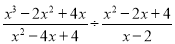 (4)
(4)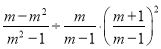
 ⑴,⑵,⑶,⑷.
【解析】试题分析:按照分式混合运算的顺序进行运算即可.
试题解析: 原式
原式
原式
原式
⑴,⑵,⑶,⑷.
【解析】试题分析:按照分式混合运算的顺序进行运算即可.
试题解析: 原式
原式
原式
原式 已知 ,则M等于( )
,则M等于( )
A.  B.
B.  C.
C.  D.
D. 
 A
【解析】试题解析:试题解析:
故选A.
A
【解析】试题解析:试题解析:
故选A. 下列变形错误的是( )
A. 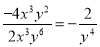 B.
B. 
C.  D.
D. 
 D
【解析】试题解析:A选项分子和分母同时除以最大公因式;B选项的分子和分母互为相反数;C选项分子和分母同时除以最大公因式,D选项正确的变形是所以答案是D选项
故选D.
D
【解析】试题解析:A选项分子和分母同时除以最大公因式;B选项的分子和分母互为相反数;C选项分子和分母同时除以最大公因式,D选项正确的变形是所以答案是D选项
故选D. 下列分式的值,可以为零的是( )
A. 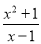 B.
B. 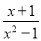 C.
C. 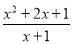 D.
D. 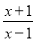
 C
【解析】A. ∵x2+1>0, ∴≠0;
B. ∵x+1=0时,x=1,此时分母x2-1=0, ∴≠0;
C. ∵x2+2x+1=0时,x=-1,此时分母x+1=0, ∴ ≠0;
D. ∵x+1=0时,x=-1,此时分母x-1≠0, ∴当x=-1时, =0.
故选D.
C
【解析】A. ∵x2+1>0, ∴≠0;
B. ∵x+1=0时,x=1,此时分母x2-1=0, ∴≠0;
C. ∵x2+2x+1=0时,x=-1,此时分母x+1=0, ∴ ≠0;
D. ∵x+1=0时,x=-1,此时分母x-1≠0, ∴当x=-1时, =0.
故选D. 下列各式变形正确的是( )
A. 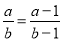 B.
B. 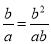 C.
C. 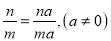 D.
D. 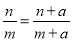
 C
【解析】A项,在原分式的分子分母上加上一个整式,等式不一定成立。故A项错误。
B项,由于b的值可能为0。故B项错误。
C项, )成立。故C项正确。
D项,在原分式的分子分母上加上一个整式,等式不一定成立。故D项错误。故本题正确答案为C。
C
【解析】A项,在原分式的分子分母上加上一个整式,等式不一定成立。故A项错误。
B项,由于b的值可能为0。故B项错误。
C项, )成立。故C项正确。
D项,在原分式的分子分母上加上一个整式,等式不一定成立。故D项错误。故本题正确答案为C。