题目内容
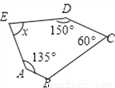
如图,已知AB∥CD,则x的度数是____________.
 75º
【解析】∵AB∥CD,
∴∠B=180°-60°=120°,
∵多边形ABCDE是五边形,
∴∠A+∠B+∠C+∠D+∠E=(5-2)×180°=540°,
∴∠E=540°-∠A-∠B-∠C-∠D=540°-135°-120°-60°-150°=75°.
75º
【解析】∵AB∥CD,
∴∠B=180°-60°=120°,
∵多边形ABCDE是五边形,
∴∠A+∠B+∠C+∠D+∠E=(5-2)×180°=540°,
∴∠E=540°-∠A-∠B-∠C-∠D=540°-135°-120°-60°-150°=75°.
练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
已知x=2时,分式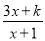 的值为零,则k=__________.
的值为零,则k=__________.
 -6
【解析】由题意得:6+k=0,解得:k=-6.
故答案:-6.
-6
【解析】由题意得:6+k=0,解得:k=-6.
故答案:-6. 下列变形错误的是( )
A. 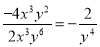 B.
B. 
C.  D.
D. 
 D
【解析】试题解析:A选项分子和分母同时除以最大公因式;B选项的分子和分母互为相反数;C选项分子和分母同时除以最大公因式,D选项正确的变形是所以答案是D选项
故选D.
D
【解析】试题解析:A选项分子和分母同时除以最大公因式;B选项的分子和分母互为相反数;C选项分子和分母同时除以最大公因式,D选项正确的变形是所以答案是D选项
故选D. 下列分式的值,可以为零的是( )
A. 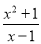 B.
B. 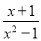 C.
C. 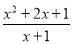 D.
D. 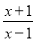
 C
【解析】A. ∵x2+1>0, ∴≠0;
B. ∵x+1=0时,x=1,此时分母x2-1=0, ∴≠0;
C. ∵x2+2x+1=0时,x=-1,此时分母x+1=0, ∴ ≠0;
D. ∵x+1=0时,x=-1,此时分母x-1≠0, ∴当x=-1时, =0.
故选D.
C
【解析】A. ∵x2+1>0, ∴≠0;
B. ∵x+1=0时,x=1,此时分母x2-1=0, ∴≠0;
C. ∵x2+2x+1=0时,x=-1,此时分母x+1=0, ∴ ≠0;
D. ∵x+1=0时,x=-1,此时分母x-1≠0, ∴当x=-1时, =0.
故选D. 一个多边形的内角和与外角和相加正好是一个九边形的内角和,试求这个多边形的边数.
 7
【解析】试题分析:设这个多边形的边数为n,根据多边形内角和与外角和定理得出(n-2) ×180º+360º=(9-2)×180º,,解之可得.
【解析】
设这个多边形的边数为n,则根据题意,
得 (n-2)·180º+360º=(9-2)×180º,
解得n=7.
所以这个多边形的边数为7.
7
【解析】试题分析:设这个多边形的边数为n,根据多边形内角和与外角和定理得出(n-2) ×180º+360º=(9-2)×180º,,解之可得.
【解析】
设这个多边形的边数为n,则根据题意,
得 (n-2)·180º+360º=(9-2)×180º,
解得n=7.
所以这个多边形的边数为7. 如图,四边形ABCD是平行四边形,点E在边BC上,如果点F是边AD上的点,那么△CDF与△ABE不一定全等的条件是( )
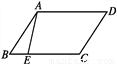
A. DF=BE B. AF=CE
C. CF=AE D. CF∥AE
 C
【解析】试题分析:A、当DF=BE时,有平行四边形的性质可得:AB=CD,∠B=∠D,利用SAS可判定△CDF≌△ABE;B、当AF=CE时,有平行四边形的性质可得:BE=DF,AB=CD,∠B=∠D,利用SAS可判定△CDF≌△ABE;C、当CF=AE时,有平行四边形的性质可得:AB=CD,∠B=∠D,利用SSA不能判定△CDF≌△ABE;D、当CF∥AE时,有平行四边形的性质可得:A...
C
【解析】试题分析:A、当DF=BE时,有平行四边形的性质可得:AB=CD,∠B=∠D,利用SAS可判定△CDF≌△ABE;B、当AF=CE时,有平行四边形的性质可得:BE=DF,AB=CD,∠B=∠D,利用SAS可判定△CDF≌△ABE;C、当CF=AE时,有平行四边形的性质可得:AB=CD,∠B=∠D,利用SSA不能判定△CDF≌△ABE;D、当CF∥AE时,有平行四边形的性质可得:A... 在□ABCD中,∠B=100°,则∠A,∠D的度数分别是( )
A. ∠A=80°,∠D=80° B. ∠A=80°,∠D=100°
C. ∠A=100°,∠D=80° D. ∠A=100°,∠D=100°
 B
【解析】∵在□ABCD中,∠B=100°,
∴∠A=180°-∠B=180°-100°=80°, ∠D=∠B=100°.
故选B.
B
【解析】∵在□ABCD中,∠B=100°,
∴∠A=180°-∠B=180°-100°=80°, ∠D=∠B=100°.
故选B. 下列各式变形正确的是( )
A. 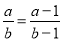 B.
B. 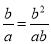 C.
C. 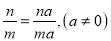 D.
D. 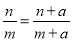
 C
【解析】A项,在原分式的分子分母上加上一个整式,等式不一定成立。故A项错误。
B项,由于b的值可能为0。故B项错误。
C项, )成立。故C项正确。
D项,在原分式的分子分母上加上一个整式,等式不一定成立。故D项错误。故本题正确答案为C。
C
【解析】A项,在原分式的分子分母上加上一个整式,等式不一定成立。故A项错误。
B项,由于b的值可能为0。故B项错误。
C项, )成立。故C项正确。
D项,在原分式的分子分母上加上一个整式,等式不一定成立。故D项错误。故本题正确答案为C。 在△ABC中,AB=AC,AD是BC边上的高,∠C=63°,BC=4,求∠BAD的度数及DC的长.
 27° 2
【解析】试题分析:根据等腰三角形的两个底角相等求出顶角∠BAC的度数,再由等腰三角形的三线合一性质即可求出∠BAD=∠BAC=27°,DC=BC=2.
试题解析:
∵AB=AC,∠C=63°,
∴∠B=∠C=63°,
∴∠BAC=180°-63°-63°=54°.
又∵AD是BC边上的高,
∴AD是∠BAC的平分线,AD是BC边上的中线,
...
27° 2
【解析】试题分析:根据等腰三角形的两个底角相等求出顶角∠BAC的度数,再由等腰三角形的三线合一性质即可求出∠BAD=∠BAC=27°,DC=BC=2.
试题解析:
∵AB=AC,∠C=63°,
∴∠B=∠C=63°,
∴∠BAC=180°-63°-63°=54°.
又∵AD是BC边上的高,
∴AD是∠BAC的平分线,AD是BC边上的中线,
...