题目内容
15. 如图,直线y=kx+b交坐标轴于A(-4,0),B(0,3),则不等式kx+b<0的解集为( )
如图,直线y=kx+b交坐标轴于A(-4,0),B(0,3),则不等式kx+b<0的解集为( )| A. | x>3 | B. | -4<x<3 | C. | x>-4 | D. | x<-4 |
分析 首先根据不等式的性质知,不等式kx+b<0的解集由一次函数的图象可知,直线y=kx+b落在x轴下方的部分所对应的x的取值,即为不等式kx+b<0的解集,从而得出结果.
解答 解:观察图象可知,当x<-4时,直线y=kx+b落在x轴的下方,
即不等式kx+b<0的解集为x<-4,
故选:D
点评 本题考查了一次函数与不等式(组)的关系及数形结合思想的应用.解决此类问题关键是仔细观察图形,注意几个关键点(交点、原点等),做到数形结合.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.方程x2+4x-6=0配方后变形为( )
| A. | (x+2)2=10 | B. | (x-2)2=10 | C. | (x+2)2=2 | D. | (x-2)2=2 |
20.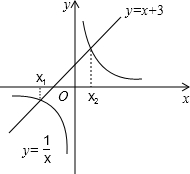 如图,方程x2+3x=1的根可看作是函数y=x+3的图象与函数y=$\frac{1}{x}$的图象交点的横坐标.类似地,利用这种图象法,可以确定方程x2+2x-1=0的实数根x0所在的范围是( )
如图,方程x2+3x=1的根可看作是函数y=x+3的图象与函数y=$\frac{1}{x}$的图象交点的横坐标.类似地,利用这种图象法,可以确定方程x2+2x-1=0的实数根x0所在的范围是( )
 如图,方程x2+3x=1的根可看作是函数y=x+3的图象与函数y=$\frac{1}{x}$的图象交点的横坐标.类似地,利用这种图象法,可以确定方程x2+2x-1=0的实数根x0所在的范围是( )
如图,方程x2+3x=1的根可看作是函数y=x+3的图象与函数y=$\frac{1}{x}$的图象交点的横坐标.类似地,利用这种图象法,可以确定方程x2+2x-1=0的实数根x0所在的范围是( )| A. | 0<x0<$\frac{1}{4}$ | B. | $\frac{1}{4}$<x0<$\frac{1}{3}$ | C. | $\frac{1}{3}$<x0<$\frac{1}{2}$ | D. | $\frac{1}{2}$<x0<1 |
7.若方程组$\left\{\begin{array}{l}{x+y=1}\\{2x+ay=b}\end{array}\right.$有唯一解,那么a,b的值应当是( )
| A. | a≠2,b为任意实数 | B. | a=2,b≠0 | C. | a=2,b≠2 | D. | a,b为任意实数 |
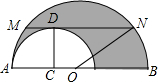 如图,在两个半圆中,大圆的弦MN与小圆相切,D为切点,且MN∥AB,MN=a,ON、CD分别为两圆的半径,求阴影部分的面积.
如图,在两个半圆中,大圆的弦MN与小圆相切,D为切点,且MN∥AB,MN=a,ON、CD分别为两圆的半径,求阴影部分的面积.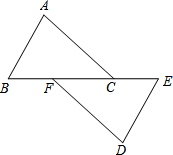 如图,已知点B、F、C、E在同一直线上,AB∥DE,AB=DE,BF=EC,试说明AC与DF平行的理由.
如图,已知点B、F、C、E在同一直线上,AB∥DE,AB=DE,BF=EC,试说明AC与DF平行的理由. 如图,在Rt△ABC中,∠ABC=90°.
如图,在Rt△ABC中,∠ABC=90°.