题目内容
5.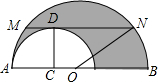 如图,在两个半圆中,大圆的弦MN与小圆相切,D为切点,且MN∥AB,MN=a,ON、CD分别为两圆的半径,求阴影部分的面积.
如图,在两个半圆中,大圆的弦MN与小圆相切,D为切点,且MN∥AB,MN=a,ON、CD分别为两圆的半径,求阴影部分的面积.
分析 如图,作OE⊥MN于E.根据切线的性质得O1D为⊙O1的半径,易得四边形OO1DC为矩形,则OC=O1D,再根据垂径定理得到AC=BC=$\frac{1}{2}$MN,在Rt△OEN中,利用勾股定理得到ON2-OE2=EN2=$\frac{1}{4}$a2,然后利用阴影部分的面积=$\frac{1}{2}$S⊙C-$\frac{1}{2}$S⊙O进行计算.
解答 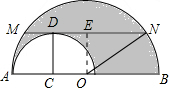 解:如图,
解:如图,
作OE⊥MN于E.
∵大半圆的弦AB与小半圆相切,
∴CD为⊙C的半径,
∴OC⊥MN,
又MN∥AB,
∴四边形DCOE为矩形,
∴OE=CD,
∵OE⊥MN,
∴ME=NE=$\frac{1}{2}$MN=$\frac{1}{2}$a,
在Rt△OEN中,ON2-OE2=EN2=$\frac{1}{4}$a2,
∴阴影部分的面积=$\frac{1}{2}$S⊙C-$\frac{1}{2}$S⊙O=$\frac{1}{2}$(π•ON2-π•CD2)=$\frac{1}{2}$π(ON2-OE2)=$\frac{π}{8}$a2.
点评 本题考查了圆的切线的性质:圆的切线垂直于经过切点的半径;经过圆心且垂直于切线的直线必经过切点.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
17.去年七八月份我市受到严重的酷热天气的影响,8月份我市某蔬菜价格呈上升趋势,其前四周每周的平均销售价格变化如表:
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接写出8月份y与x 的函数关系式;
(2)进入9月,由于本地蔬菜的上市,此种蔬菜的平均销售价格y(元/千克)从9月第1周的2.8元/千克下降至第2周的2.4元/千克,且y与周数x的变化情况满足二次函数y=-$\frac{1}{20}$x2+bx+c,请求出9月份y与x的函数关系式;
(3)若8月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=$\frac{1}{4}$x+1.2,9月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=$-\frac{1}{5}$x+2.试问8月份与9月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
(4)若9月份的第2周共销售100吨此种蔬菜.从9月份第3周起,由于受暴雨的影响,此种蔬菜的可供销量将在第2周销量的基础上每周减少a%,政府为稳定蔬菜价格,从外地调运2吨此种蔬菜,刚好满足本地市民的需要,且使此种蔬菜的销售价格比第2周仅上涨0.8a%.若在这一举措下,此种蔬菜在第3周的总销售额与第2周刚好持平,请你参考以下数据,通过计算估算出a的整数值.
(参考数据:372=1369,382=1444,392=1521,402=1600,412=1681)
| 周数x | 1 | 2 | 3 | 4 |
| 价格y(元/千克) | 2 | 2.2 | 2.4 | 2.6 |
(2)进入9月,由于本地蔬菜的上市,此种蔬菜的平均销售价格y(元/千克)从9月第1周的2.8元/千克下降至第2周的2.4元/千克,且y与周数x的变化情况满足二次函数y=-$\frac{1}{20}$x2+bx+c,请求出9月份y与x的函数关系式;
(3)若8月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=$\frac{1}{4}$x+1.2,9月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=$-\frac{1}{5}$x+2.试问8月份与9月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
(4)若9月份的第2周共销售100吨此种蔬菜.从9月份第3周起,由于受暴雨的影响,此种蔬菜的可供销量将在第2周销量的基础上每周减少a%,政府为稳定蔬菜价格,从外地调运2吨此种蔬菜,刚好满足本地市民的需要,且使此种蔬菜的销售价格比第2周仅上涨0.8a%.若在这一举措下,此种蔬菜在第3周的总销售额与第2周刚好持平,请你参考以下数据,通过计算估算出a的整数值.
(参考数据:372=1369,382=1444,392=1521,402=1600,412=1681)
14.近年来,全国房价不断上涨,某市201 4年4月份的房价平均每平方米为6600元,比2012年同期的房价平均每平方米上涨了2000元,假设这两年该市房价的平均增长率均为x,则关于x的方程为( )
| A. | (1+x)2=2000 | B. | 2000(1+x)2=6600 | ||
| C. | (6600-200)(1+x)=6600 | D. | (6600-2000)(1+x)2=6600 |
15. 如图,直线y=kx+b交坐标轴于A(-4,0),B(0,3),则不等式kx+b<0的解集为( )
如图,直线y=kx+b交坐标轴于A(-4,0),B(0,3),则不等式kx+b<0的解集为( )
 如图,直线y=kx+b交坐标轴于A(-4,0),B(0,3),则不等式kx+b<0的解集为( )
如图,直线y=kx+b交坐标轴于A(-4,0),B(0,3),则不等式kx+b<0的解集为( )| A. | x>3 | B. | -4<x<3 | C. | x>-4 | D. | x<-4 |
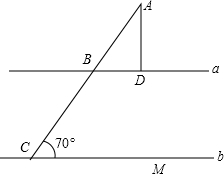 如图所示,已知a∥b,AD⊥直线a,求∠A的度数.
如图所示,已知a∥b,AD⊥直线a,求∠A的度数.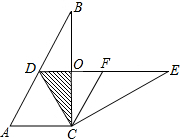 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上,DE交BC于点O.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上,DE交BC于点O.