题目内容
20.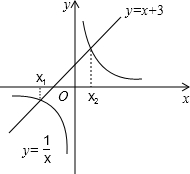 如图,方程x2+3x=1的根可看作是函数y=x+3的图象与函数y=$\frac{1}{x}$的图象交点的横坐标.类似地,利用这种图象法,可以确定方程x2+2x-1=0的实数根x0所在的范围是( )
如图,方程x2+3x=1的根可看作是函数y=x+3的图象与函数y=$\frac{1}{x}$的图象交点的横坐标.类似地,利用这种图象法,可以确定方程x2+2x-1=0的实数根x0所在的范围是( )| A. | 0<x0<$\frac{1}{4}$ | B. | $\frac{1}{4}$<x0<$\frac{1}{3}$ | C. | $\frac{1}{3}$<x0<$\frac{1}{2}$ | D. | $\frac{1}{2}$<x0<1 |
分析 方程x2+2x-1=0的实数根可以看作函数y=x+2和y=$\frac{1}{x}$的交点,判断各个选项中的分点对应的点是否在交点的同侧还是异侧即可判断.
解答  解:方程x2+2x-1=0的实数根可以看作函数y=x+2和y=$\frac{1}{x}$的交点.
解:方程x2+2x-1=0的实数根可以看作函数y=x+2和y=$\frac{1}{x}$的交点.
函数大体图象是:
当x0表示第一象限交点的横坐标时,
A、当x=$\frac{1}{4}$时,一次函数的值时$\frac{9}{2}$,反比例函数的值是4,则x=$\frac{1}{4}$一定在交点的左侧,故选项错误;
B、当x=$\frac{1}{4}$时,一次函数的值时$\frac{9}{2}$,反比例函数的值是4,则x=$\frac{1}{4}$一定在交点的左侧;
同理,当x=$\frac{1}{3}$时,一定在交点的左侧,故选项错误;
C、当x=$\frac{1}{3}$时,一定在交点的左侧,当x=$\frac{1}{2}$时,一次函数的值大于反比例函数的值,则一定在交点的右侧,故选项正确;
D、同理可证当x=$\frac{1}{2}$和x=1时都在交点的右侧,则选项错误.
故选C.
点评 本题考查了一元二次方程和一次函数以及反比例函数之间的关系,注意数形结合思想的应用是关键.

练习册系列答案
相关题目
8.甲、乙两个工程队各自维修2800米的路面,甲工程队每小时维修路面的速度是乙工程队每小时维修路面速度的4倍,结果甲比乙早2小时完成了任务.设乙工程队每小时维修路面x米,则下面所列方程正确的是( )
| A. | $\frac{2800}{x}$-$\frac{2800}{5x}$=2 | B. | $\frac{2800}{5x}$-$\frac{2800}{x}$=2 | C. | $\frac{2800}{x}$-$\frac{2800}{4x}$=2 | D. | $\frac{2800}{4x}$-$\frac{2800}{x}$=2 |
15. 如图,直线y=kx+b交坐标轴于A(-4,0),B(0,3),则不等式kx+b<0的解集为( )
如图,直线y=kx+b交坐标轴于A(-4,0),B(0,3),则不等式kx+b<0的解集为( )
 如图,直线y=kx+b交坐标轴于A(-4,0),B(0,3),则不等式kx+b<0的解集为( )
如图,直线y=kx+b交坐标轴于A(-4,0),B(0,3),则不等式kx+b<0的解集为( )| A. | x>3 | B. | -4<x<3 | C. | x>-4 | D. | x<-4 |
9.为了加强公民的节水意识,合理利用水资源,各地采用价格调控手段达到节约用水的目的.某市规定如下用水收费标准:每户每月的用水量不超过6立方米时,水费按每立方米a元收费,超过6立方米时,不超过的部分,每立方米仍按a元收费,超过的部分,每立方米按c元收费,该市某户今年四五月份的用水量和所交水费如下表所示:涉牧户每月用水量x立方厘米,应交水费y元.
为了加强公民的节水意识,合理利用水资源,各地采用价格调控等手段达到节约用水的目的.某市规定如下用水收费标准:每户每月的用水不超过6立方米时,水费按每立方米a元收费;超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按c元收费.该市某户今年4,5月份的用水量和水费如下表所示:
设某户该月用水量为x(立方米),应交水费y(元).
(1)求a,c的值;
(2)当x≤6,x≥6时,分别写出y于x的函数关系式;
(3)若该户6月份的用水量为8立方米,求该户6月份的水费是多少元?
为了加强公民的节水意识,合理利用水资源,各地采用价格调控等手段达到节约用水的目的.某市规定如下用水收费标准:每户每月的用水不超过6立方米时,水费按每立方米a元收费;超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按c元收费.该市某户今年4,5月份的用水量和水费如下表所示:
| 月份 | 用水量(m3) | 收费(元) |
| 3 | 5 | 7.5 |
| 4 | 9 | 27 |
(1)求a,c的值;
(2)当x≤6,x≥6时,分别写出y于x的函数关系式;
(3)若该户6月份的用水量为8立方米,求该户6月份的水费是多少元?
10.为了满足市场需求,某厂家生产A、B两种款式的环保购物袋,每天共生产5000个,两种购物袋的成本和售价如下表
设每天生产A种购物袋x个,每天共获利y元
(1)求y与x的函数解析式;
(2)如果该厂每天最多投入成本12000元,那么每天最多获利多少元?
| 成本(元/个) | 售价 (元/个) | |
| A | 2 | 2.4 |
| B | 3 | 3.6 |
(1)求y与x的函数解析式;
(2)如果该厂每天最多投入成本12000元,那么每天最多获利多少元?
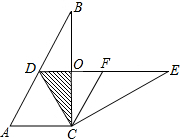 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上,DE交BC于点O.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上,DE交BC于点O. 正方形ABCD的边AD上有一点E,满足BE=ED+DC,如果M是AD的中点,求证:∠EBC=2∠ABM.
正方形ABCD的边AD上有一点E,满足BE=ED+DC,如果M是AD的中点,求证:∠EBC=2∠ABM.