题目内容
13．矩形ABCD的对角线AC，BD交于点O，∠AOB=60°，AB=4，矩形ABCD的面积为16$\sqrt{3}$．分析 由矩形的性质得出AO=BO=$\frac{1}{2}$BD，再证明△AOB为等边三角形，得出BO=AB，求出BD，由勾股定理求出AD，即可得出结果．
解答 解：如图所示：
∵四边形ABCD是矩形，
∴AO=BO=$\frac{1}{2}$BD，∠BAD=90°，
又∵∠AOB=60°，
∴△AOB为等边三角形，
∴BO=AB=4，
∴BD=2BO=8，
∴AD=$\sqrt{B{D}^{2}-A{B}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$，
∴矩形ABCD的面积=AB×AD=4×4$\sqrt{3}$=16$\sqrt{3}$；
故答案为：16$\sqrt{3}$．
点评 本题考查了矩形的性质、等边三角形的判定与性质、勾股定理；熟练掌握矩形的性质，证明三角形是等边三角形是解决问题的关键．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
导学与测试系列答案
相关题目
16．
二次函数y=ax2+bx+c的图象如图所示，则下列关系式错误的是（ ）
二次函数y=ax2+bx+c的图象如图所示，则下列关系式错误的是（ ）| A． | a＞0 | B． | c＞0 | C． | b2-4ac＞0 | D． | a+b+c＞0 |
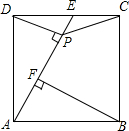如图，正方形ABCD中，点E为CD的中点，DP⊥AE，垂足为P点，BF⊥AE于F，
已知：如图，在△ABC中，AB=BC=2，∠ABC=120°，BC∥x轴，点B的坐标是（-3，1）．△ABC关于y轴对称的△A′B′C′；则以A、B、B′、A′为顶点的四边形的面积7$\sqrt{3}$．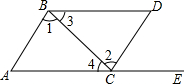
如图，点E在AC的延长线上，下列条件①∠3=∠4，②∠1=∠2，③∠D=∠ACD，④∠D+∠ACD=180°中，能判断AB∥CD的是②（填序号即可）．
已知：如图，平行四边形ABCD的对角线相交于点O，点E在边BC的延长线上，且OE=OB，连接DE．求证：DE⊥BE．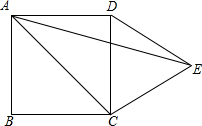
如图，在正方形ABCD的外侧作等边三角形DCE，则∠EAC的度数为30°．