Question

4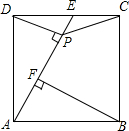．如图，正方形ABCD中，点E为CD的中点，DP⊥AE，垂足为P点，BF⊥AE于F，
（1）求证：AF=PF；
（2）连CP，若AB=2$\sqrt{5}$，求CP的长；
（3）若点E为DC边上一动点，DP⊥AE，当点E从D点运动到点C时，求点P运动的路径与AB之比．

Answer 1

分析 （1）要证AF=PF，先延长BF交AD于G，然后可以证△ADE≌△BAG．从而G为AD中点，又BG平行于PD，因此F为AP中点．即AF=PF．
（2）要求PC的长，过点P作垂线PH垂直CD于点H．根据三角形的相似：△DEP～△AED关系，得出$\frac{EH}{ED}=\frac{HP}{DA}$=$\frac{EP}{EA}$，PE=1，PH=$\frac{2}{5}\sqrt{5}$，CH=$\frac{6}{5}\sqrt{5}$，由勾股定理，CP=$2\sqrt{2}$，
（3）结合图形不难得出，当点E运动到点C时，点P与点F重合，即P为对角线BD的中点，点P的运动轨迹是弧．

解答 （1）证明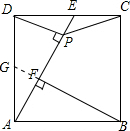：先延长BF交AD于G，
在正方形ABCD中，∵∠GAB=90
∴∠DAE+∠EAB=90°，
∵BF⊥AE于点F，
∴∠EAB+∠GBA=90°，
∴∠DAE=∠GBA，
∵∠EDA=∠GAB=90°，AD=AB，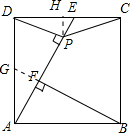
∴△ADE≌△BAG．
∴AG=DE=$\frac{1}{2}$DC=$\frac{1}{2}$AD，
∵DP⊥AE，BF⊥AE，
∴DP∥BF，
∴点F为AP的中点，即AF=PF．
（2）解：过点P作PH⊥DC于点H，
∵∠ADE=90°，AD=2$\sqrt{5}$，DE=$\frac{1}{2}$DC=$\sqrt{5}$，$\frac{EH}{ED}=\frac{HP}{DA}$
∴AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\sqrt{（2\sqrt{5}）^{2}+（\sqrt{5}）^{2}}$=5，
DE²=EP•AE，
（$\sqrt{5}$）²=EP•5，
∴EP=1
又∵AD⊥DC，
∴△DEP～△AED
∴$\frac{EH}{ED}=\frac{HP}{DA}$=$\frac{EP}{EA}$
∴$\frac{HE}{\sqrt{5}}=\frac{HP}{2\sqrt{5}}=\frac{1}{5}$，
∴PH=$\frac{2}{5}\sqrt{5}$，HE=$\frac{1}{5}\sqrt{5}$，
∴CH=CE+HE=$\frac{6}{5}\sqrt{5}$，
∴PC=$\sqrt{H{P}^{2}+H{C}^{2}}$=$\sqrt{（\frac{2}{5}\sqrt{5}）^{2}+（\frac{6}{5}\sqrt{5}）^{2}}$=2$\sqrt{2}$，
（3）解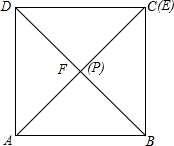：点E与D重合时，点P与点E重合；当点E从D运动到点C时，点P从E向点A运动，且当点E与C重合时，点P与F重合且为对角线DB的中点．点P的运动轨迹是弧，设AB=2a，
弧长=$\frac{1}{4}$•2π•a=$\frac{πa}{2}$，
∴点P运动的路径与AB之比=$\frac{πa}{2}$：2a=$\frac{π}{4}$．

点评 本题主要考查全等三角形的判定方法及动点问题，由正方形的性质得到边相等，再利用全等三角形的判定证明三角形全等是解题的关键．动点问题要结合图形，根据点的运动特征是正确求解的关键．