Question

2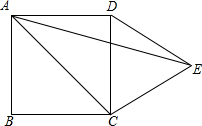．如图，在正方形ABCD的外侧作等边三角形DCE，则∠EAC的度数为30°．

Answer 1

分析 先根据正方形的性质求得∠DAC的度数，再根据等腰三角形中∠ADE的度数求得∠DAE的度数，最后根据∠EAC=∠DAC-∠DAE，进行计算即可．

解答 解：∵正方形ABCD中，∠DAC=45°，∠ADC=90°
等边三角形DCE中，∠CDE=60°，
∴∠ADE=150°，
又∵AD=CD=DE，
∴等腰三角形ADE中，∠DAE=$\frac{180°-150°}{2}$=15°，
∴∠EAC=∠DAC-∠DAE=45°-15°=30°．
故答案为：30°．

点评 本题主要考查了正方形的性质以及等边三角形的性质，解题时注意：△ADE为等腰三角形，其底角的度数等于180°减去顶角的度数，再除以2．