题目内容
11. 如图,在△ABC中,∠BAC=90°,AB=8,AC=6,线段BC所在的直线以每秒2个单位的速度,沿与其垂直的方向向上平行移动,设x秒时,该直线在△ABC内部的部分DE的长度为y,试写出y关于x的函数关系式.
如图,在△ABC中,∠BAC=90°,AB=8,AC=6,线段BC所在的直线以每秒2个单位的速度,沿与其垂直的方向向上平行移动,设x秒时,该直线在△ABC内部的部分DE的长度为y,试写出y关于x的函数关系式.
分析 首先该直线与AB交于D,与AC交于E,由DE∥BC,即可得 $\frac{AG}{AF}$=$\frac{DE}{BC}$,然后可求得y关于x的函数关系式.
解答 解:过A作AF⊥BC,该直线与AB交于D,与AC交于E,AF为BC边上的高,
∵AB=8,AC=6,∠BAC=90°
∴BC=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵S△ABC=$\frac{1}{2}$•AB•AC=$\frac{1}{2}$•BC•AF,
∴AF=$\frac{6×8}{10}$=$\frac{24}{5}$,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AG}{AF}$=$\frac{DE}{BC}$,
∵FG=2x,
∴AG=$\frac{24}{5}$-2x,
∴$\frac{\frac{24}{5}-2x}{\frac{24}{5}}$=$\frac{y}{10}$,
解得:y=-$\frac{25}{6}$x+10(0<x<$\frac{12}{5}$).
答:y关于x的函数关系式为:y=-$\frac{25}{6}$x+10(0<x<$\frac{12}{5}$).
点评 此题考查了相似三角形的判定与性质.此题难度适中,注意掌握相似三角形的对应边成比例定理的应用是解此题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
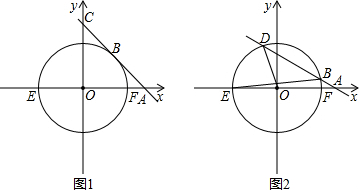
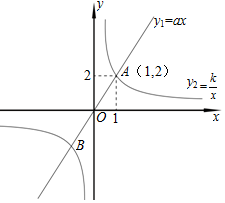 如图,已知正比例函数y1=ax的图象与反比例函数y2=$\frac{k}{x}$ 的图象有一个公共点A(1,2).
如图,已知正比例函数y1=ax的图象与反比例函数y2=$\frac{k}{x}$ 的图象有一个公共点A(1,2).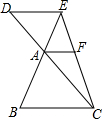 如图,若BC∥DE∥AF 则下列结论中:
如图,若BC∥DE∥AF 则下列结论中: 如图,将边长为4的正方形ABCD沿其对角线AC剪开,固定△ADC,并把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为2时,它移动的距离AA′等于2+$\sqrt{2}$或2-$\sqrt{2}$.
如图,将边长为4的正方形ABCD沿其对角线AC剪开,固定△ADC,并把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为2时,它移动的距离AA′等于2+$\sqrt{2}$或2-$\sqrt{2}$.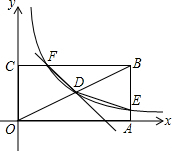 如图,矩形OABC的顶点A,C分别在x,y轴的正半轴上,D为对角线OB的中点,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点D,且与AB、BC分别交于点E,F,点B的坐标为(2$\sqrt{3}$,2).
如图,矩形OABC的顶点A,C分别在x,y轴的正半轴上,D为对角线OB的中点,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点D,且与AB、BC分别交于点E,F,点B的坐标为(2$\sqrt{3}$,2).