题目内容
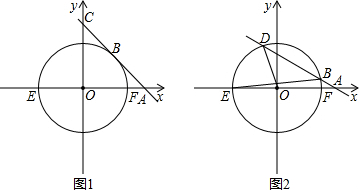
1.平面直角坐标系中,半径为2的⊙O交x轴于E、F两点,过点A(4,0)的直线与y轴相交于点C.(1)如图1,当直线AC与⊙O相切于点B时:
①求AB的长;②求直线AC的函数关系式.
(2)如图2,将直线AC绕点A逆时针转过一定角度,与⊙O交于点B、D,连接EB、OD,当AB=BD时:
①判断OD与EB的位置关系,并说明理由;②求出AD的长.
分析 (1)①先求出OB,利用勾股定理即可求出AB,
②先求出∠OAB=30°,利用锐角三角函数求出OC,最后用待定系数法即可得出结论;
(2)①先判断出∠EBF=90°,再判断出BF是△AOD的中位线,即可得出BF∥OD即可得出结论;
②先判断出△ABF∽△AED,得出比例式即可求出AB,即可得出结论.
解答 解:(1)①如图1,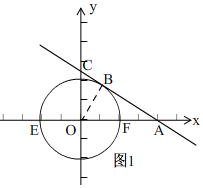
连接OB,∵直线AC与⊙O相切于点B,
∴∠ABO=90°,
∵A(4,0),
∴OA=4,
∵⊙O半径为2,
∴AB=2$\sqrt{3}$,
②由①知,在Rt△ABO中,OA=4,OB=2,
∴sin∠OAB=$\frac{OB}{OA}$=$\frac{1}{2}$,
∴∠OAB=30°,
在Rt△AOC中,∠OAB=30°,OB=4,
∴OC=OB•tan∠OAB=4×$\frac{\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$,
设直线AC的解析式y=kx+$\frac{4\sqrt{3}}{3}$,
∵A(4,0),
∴4k+$\frac{4\sqrt{3}}{3}$=0,
∴k=-$\frac{\sqrt{3}}{3}$,
∴直线AC的解析式为y=-$\frac{\sqrt{3}}{3}$x+$\frac{4\sqrt{3}}{3}$;
(2)①OD⊥BE,理由:如图2,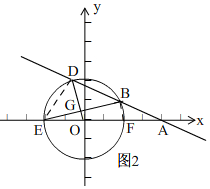
连接BF,∵EF是⊙O的直径,
∴∠EBF=90°,OF=2,
∵OA=4,
∴AF=OF=2,
∵点B时AD的中点,
∴BF是△AOD的中位线,
∴BF∥OD,
∴∠BGD=∠EBF=90°,
∴OD⊥BE,
②连接DE,∵四边形BDEF是⊙O的内接四边形,
∴∠AFB=∠ADE,
∵∠BAF=∠EAD,
∴△ABF∽△AED,
∴$\frac{AB}{AE}=\frac{AF}{AD}$,
∵AF=2,AE=6,AD=2AB,
∴$\frac{AB}{6}=\frac{2}{2AB}$,
∴AB=$\sqrt{6}$,
∴AD=2AB=2$\sqrt{6}$.
点评 此题是一次函数综合题,主要考查了圆的切线的性质,直角三角形的性质,锐角三角函数,三角形的中位线,相似三角形的判定和性质,待定系数法,解(1)的关键是求出∠OAB,解(2)的关键是判断出BF时△OAD的中位线.

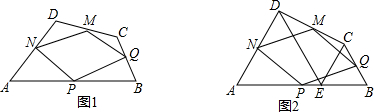
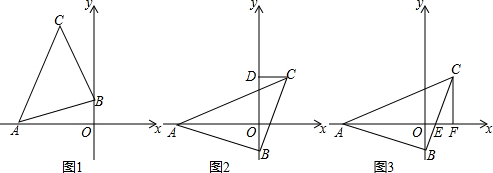
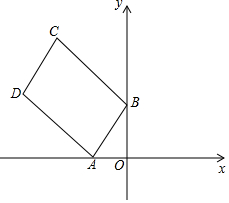 如图,在直角坐标系中,点A,B分别在x轴负半轴、y轴正半轴上,
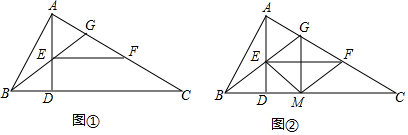
如图,在直角坐标系中,点A,B分别在x轴负半轴、y轴正半轴上, 如图,在△ABC中,∠BAC=90°,AB=8,AC=6,线段BC所在的直线以每秒2个单位的速度,沿与其垂直的方向向上平行移动,设x秒时,该直线在△ABC内部的部分DE的长度为y,试写出y关于x的函数关系式.
如图,在△ABC中,∠BAC=90°,AB=8,AC=6,线段BC所在的直线以每秒2个单位的速度,沿与其垂直的方向向上平行移动,设x秒时,该直线在△ABC内部的部分DE的长度为y,试写出y关于x的函数关系式.