题目内容
6. 如图,将边长为4的正方形ABCD沿其对角线AC剪开,固定△ADC,并把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为2时,它移动的距离AA′等于2+$\sqrt{2}$或2-$\sqrt{2}$.
如图,将边长为4的正方形ABCD沿其对角线AC剪开,固定△ADC,并把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为2时,它移动的距离AA′等于2+$\sqrt{2}$或2-$\sqrt{2}$.
分析 设AA′=x,AC与A′B′相交于点E,判断出△AA′E是等腰直角三角形,根据等腰直角三角形的性质可得A′E=x,再表示出A′D,然后根据平行四边形的面积公式列方程求解即可.
解答 解:设AA′=x,AC与A′B′相交于点E
∵△ACD是正方形ABCD剪开得到的,
∴△ACD是等腰直角三角形,
∴∠A=45°,
∴△AA′E是等腰直角三角形,
∴A′E=AA′=x,
A′D=AD-AA′=4-x,
∵两个三角形重叠部分的面积为2,
∴x(4-x)=2,
整理得,x2-4x+2=0,
解得x1=2+$\sqrt{2}$,x2=2-$\sqrt{2}$,
即移动的距离AA′为2+$\sqrt{2}$或2-$\sqrt{2}$.
故答案为2+$\sqrt{2}$或2-$\sqrt{2}$.
点评 本题考查了平移的性质,正方形的性质,等腰直角三角形的判定与性质,熟记平移的性质并用平移距离表示出重叠部分的底与高是解题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
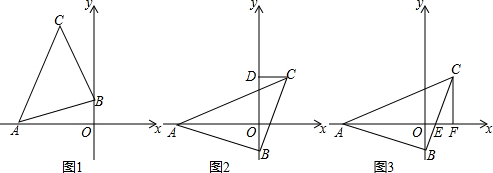
 求值:某小区有一块长为(3a+b)米,宽为(2a+b)米的长方形地块(如图所示),物业公司计划将中间修建一小型喷泉,然后将周围(阴影部分)进行绿化;
求值:某小区有一块长为(3a+b)米,宽为(2a+b)米的长方形地块(如图所示),物业公司计划将中间修建一小型喷泉,然后将周围(阴影部分)进行绿化; 如图,在△ABC中,∠BAC=90°,AB=8,AC=6,线段BC所在的直线以每秒2个单位的速度,沿与其垂直的方向向上平行移动,设x秒时,该直线在△ABC内部的部分DE的长度为y,试写出y关于x的函数关系式.
如图,在△ABC中,∠BAC=90°,AB=8,AC=6,线段BC所在的直线以每秒2个单位的速度,沿与其垂直的方向向上平行移动,设x秒时,该直线在△ABC内部的部分DE的长度为y,试写出y关于x的函数关系式.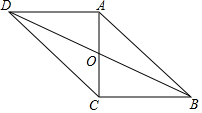 如图,在?ABCD中,对角线AC、BD交于点O,AC⊥BC,且?ABCD的周长为36,△OCD的周长比△OBC的周长大2.
如图,在?ABCD中,对角线AC、BD交于点O,AC⊥BC,且?ABCD的周长为36,△OCD的周长比△OBC的周长大2.