题目内容
20.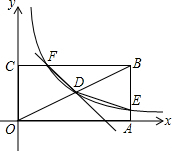 如图,矩形OABC的顶点A,C分别在x,y轴的正半轴上,D为对角线OB的中点,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点D,且与AB、BC分别交于点E,F,点B的坐标为(2$\sqrt{3}$,2).
如图,矩形OABC的顶点A,C分别在x,y轴的正半轴上,D为对角线OB的中点,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点D,且与AB、BC分别交于点E,F,点B的坐标为(2$\sqrt{3}$,2).(1)求反比例函数的解析式;
(2)连接DE,求△BDE的面积;
(3)直接写出在第一象限内当x满足什么条件时,直线FD的函数值大于反比例函数y=$\frac{k}{x}$的函数值.
分析 (1)先根据点D为对角线OB的中点,求出D点坐标,代入反比例函数,即可得出k的值;
(2)先求得点E的坐标,过点D作DH⊥AB于H,进而根据S△BDE=$\frac{1}{2}$BE×DH进行计算即可;
(3)先求得点F的坐标,再根据D($\sqrt{3}$,1),即可得出当一次函数值大于反比例函数y=$\frac{k}{x}$的函数值时,x的取值范围.
解答 解:(1)∵B(2$\sqrt{3}$,2),点D为对角线OB的中点,
∴D($\sqrt{3}$,1),
∵点D在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,
∴k=$\sqrt{3}$×1=$\sqrt{3}$,
∴反比例函数的关系式为:y=$\frac{\sqrt{3}}{x}$;
(2)设点E的坐标为(2$\sqrt{3}$,m),代入y=$\frac{\sqrt{3}}{x}$,可得m=$\frac{1}{2}$,
∴BE=2-$\frac{1}{2}$=$\frac{3}{2}$,
如图,过点D作DH⊥AB于H,则DH=$\frac{1}{2}$AO=$\sqrt{3}$,
∴S△BDE=$\frac{1}{2}$BE×DH=$\frac{1}{2}$×$\frac{3}{2}$×$\sqrt{3}$=$\frac{3}{4}\sqrt{3}$;
(3)设点F的坐标为(n,2),代入y=$\frac{\sqrt{3}}{x}$,可得n=$\frac{\sqrt{3}}{2}$,
∴F($\frac{\sqrt{3}}{2}$,2),
又∵D($\sqrt{3}$,1),
∴在第一象限内,当一次函数值大于反比例函数y=$\frac{k}{x}$的函数值时,x的取值范围为:$\frac{\sqrt{3}}{2}$<x<$\sqrt{3}$.
点评 本题考查的是反比例函数与一次函数交点问题,涉及到反比例函数图象上点的坐标特点、矩形的性质、三角形的面积等知识,解决问题的关键是掌握:矩形的对角相等且互相平分;解题时注意数形结合思想的运用.

| A | B | |
| 进价(万元/套) | 1.5 | 1.2 |
| 售价(万元/套) | 1.65 | 1.4 |
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少的数量的1.5倍.若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?
(3)在(2)的条件下,该商场所能获得的最大利润是多少万元?
 某体育用品商场为了推销一种品牌运动服,先做了市场调查,得到数据如下表:
某体育用品商场为了推销一种品牌运动服,先做了市场调查,得到数据如下表:| 卖出价格x(元/件) | 50 | 51 | 52 | 53 |
| 销售量p(件) | 500 | 490 | 480 | 470 |
(2)如果这种运动服的买入价为每件40元,试求销售利润y(元)与卖出价格x(元/件)的函数关系式(销售利润=销售收入-买入支出);
(3)在(2)的条件下,当卖出价为多少时,能获得最大利润?最大利润为多少?
 如图,在△ABC中,∠BAC=90°,AB=8,AC=6,线段BC所在的直线以每秒2个单位的速度,沿与其垂直的方向向上平行移动,设x秒时,该直线在△ABC内部的部分DE的长度为y,试写出y关于x的函数关系式.
如图,在△ABC中,∠BAC=90°,AB=8,AC=6,线段BC所在的直线以每秒2个单位的速度,沿与其垂直的方向向上平行移动,设x秒时,该直线在△ABC内部的部分DE的长度为y,试写出y关于x的函数关系式.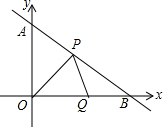 如图,直线y=-$\frac{3}{4}$x+3与y轴交于点A,与x轴交于点B,点P从点B出发以每秒1个单位长度的速度沿BA边向终点A运动,同时点Q以相同的速度从坐标原点O出发沿OB边向终点B运动,设点P运动的时间为t秒.
如图,直线y=-$\frac{3}{4}$x+3与y轴交于点A,与x轴交于点B,点P从点B出发以每秒1个单位长度的速度沿BA边向终点A运动,同时点Q以相同的速度从坐标原点O出发沿OB边向终点B运动,设点P运动的时间为t秒.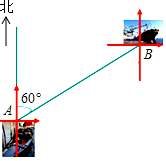 天气晴朗时,一个人能看到大海的最远距离s(单位:km)可用公式s2=16.9h来估计,其中h(单位:m)是眼睛离海平面的高度.
天气晴朗时,一个人能看到大海的最远距离s(单位:km)可用公式s2=16.9h来估计,其中h(单位:m)是眼睛离海平面的高度.