题目内容
2.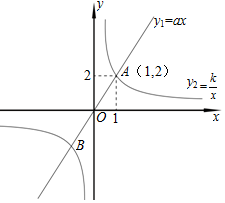 如图,已知正比例函数y1=ax的图象与反比例函数y2=$\frac{k}{x}$ 的图象有一个公共点A(1,2).
如图,已知正比例函数y1=ax的图象与反比例函数y2=$\frac{k}{x}$ 的图象有一个公共点A(1,2).(1)求这两个函数表达式;
(2)根据图象写出正比例函数值大于反比例函数值的x的取值范围;
(3)根据反比例函数的图象,写出当-2<x<-1时y2的取值范围.
分析 (1)根据点A的坐标,利用待定系数法即可求出正(反)比例函数表达式;
(2)由两函数图象的对称性可得出点B的坐标,再根据两函数图象的上下位置关系,即可找出正比例函数值大于反比例函数值的x的取值范围;
(3)根据反比例函数的性质找出在-2<x<-1上,y值随x值的增大而减小,再根据反比例函数图象上点的坐标特征,即可找出当-2<x<-1时y2的取值范围.
解答 解:(1)将点A(1,2)代入y1=ax中,
2=a×1,解得:a=2,
∴正比例函数表达式为y1=2x.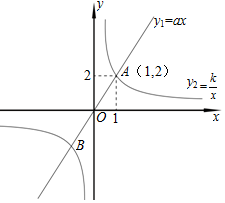
将点A(1,2)代入y2=$\frac{k}{x}$中,
2=$\frac{k}{1}$,解得:k=2,
∴反比例函数表达式为y2=$\frac{2}{x}$.
(2)由正、反比例函数图象的对称性可知:点B的坐标为(-1,-2).
观察函数图象可知:当-1<x<0或x>1时,正比例函数图象在反比例函数图象上方,
∴正比例函数值大于反比例函数值的x的取值范围为-1<x<0或x>1.
(3)∵k=2>0,
∴在-2<x<-1上,y值随x值的增大而减小.
当x=-2时,y2=$\frac{2}{x}$=-1;
当x=-1时,y2=$\frac{2}{x}$=-2.
∴当-2<x<-1时y2的取值范围为-2<y2<-1.
点评 本题考查了反比例函数与一次函数的交点问题、待定系数法求正比例函数解析式、待定系数法求反比例函数解析式以及反比例函数图象上点的坐标特征,解题的关键是:(1)根据点A的坐标,利用待定系数法求出正(反)比例函数关系式;(2)根据两函数图象的上下位置关系找出正比例函数值大于反比例函数值的x的取值范围;(3)根据反比例函数的性质结合反比例函数图象上点的坐标特征,求出当-2<x<-1时y2的取值范围.

练习册系列答案
相关题目
12.佳润商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如表所示:
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元.
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少的数量的1.5倍.若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?
(3)在(2)的条件下,该商场所能获得的最大利润是多少万元?
| A | B | |
| 进价(万元/套) | 1.5 | 1.2 |
| 售价(万元/套) | 1.65 | 1.4 |
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少的数量的1.5倍.若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?
(3)在(2)的条件下,该商场所能获得的最大利润是多少万元?
 如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合), 求值:某小区有一块长为(3a+b)米,宽为(2a+b)米的长方形地块(如图所示),物业公司计划将中间修建一小型喷泉,然后将周围(阴影部分)进行绿化;
求值:某小区有一块长为(3a+b)米,宽为(2a+b)米的长方形地块(如图所示),物业公司计划将中间修建一小型喷泉,然后将周围(阴影部分)进行绿化; 如图,在△ABC中,∠BAC=90°,AB=8,AC=6,线段BC所在的直线以每秒2个单位的速度,沿与其垂直的方向向上平行移动,设x秒时,该直线在△ABC内部的部分DE的长度为y,试写出y关于x的函数关系式.
如图,在△ABC中,∠BAC=90°,AB=8,AC=6,线段BC所在的直线以每秒2个单位的速度,沿与其垂直的方向向上平行移动,设x秒时,该直线在△ABC内部的部分DE的长度为y,试写出y关于x的函数关系式.