题目内容
9.若不等式$\frac{1}{2}$x<2的解集都能使关于x的一次不等式(a-3)x<a+5成立,则a的取值范围是3<a≤$\frac{17}{3}$.分析 先求出x的取值范围,再由不等式的基本性质即可得出a的取值范围.
解答 解:解不等式$\frac{1}{2}$x<2得,x<4.
∵不等式$\frac{1}{2}$x<2的解集都能使关于x的一次不等式(a-3)x<a+5成立,
∴$\left\{\begin{array}{l}a-3>0\\ \frac{a+5}{a-3}≥4\end{array}\right.$,解得3<a≤$\frac{17}{3}$.
故答案为:3<a≤$\frac{17}{3}$.
点评 本题考查的是不等式的解集,根据题意得出关于a的不等式组是解答此题的关键.

练习册系列答案
相关题目
20.某商场有A、B两种商品,每件的进价分别为15元、35元.商场销售5件A商品和1件B商品,可获得利润35元;销售6件A商品和3件B商品,可获得利润60元.
(1)求A、B两种商品的销售单价;
(2)如果该商场计划最多投入2 000元用于购进A、B两种商品共80件,那么购进A种商品的件数应满足怎样的条件?
(3)现该商场对A、B两种商品进行优惠促销,优惠措施如表所示:
如果一次性付款432元同时购买A、B两种商品,求商场获得的最小利润和最大利润.
(1)求A、B两种商品的销售单价;
(2)如果该商场计划最多投入2 000元用于购进A、B两种商品共80件,那么购进A种商品的件数应满足怎样的条件?
(3)现该商场对A、B两种商品进行优惠促销,优惠措施如表所示:
| 打折前一次性购物总金额 | 优惠措施 |
| 不超过500元 | 售价打九折 |
| 超过500元 | 售价打八折 |

 如图,为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,给出如下的判断:
如图,为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,给出如下的判断: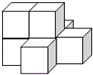 如图是一个由7个同样的立方体叠成的几何体,请问下列选项中,既是中心对称图形,又是这个几何体的三视图之一的是( )
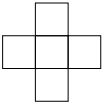
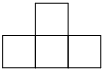
如图是一个由7个同样的立方体叠成的几何体,请问下列选项中,既是中心对称图形,又是这个几何体的三视图之一的是( )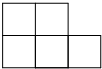

 如图,△ABC和△AMN均为等边三角形,将△AMN绕点A旋转(△AMN在直线AC的右侧).
如图,△ABC和△AMN均为等边三角形,将△AMN绕点A旋转(△AMN在直线AC的右侧).