题目内容
20.某商场有A、B两种商品,每件的进价分别为15元、35元.商场销售5件A商品和1件B商品,可获得利润35元;销售6件A商品和3件B商品,可获得利润60元.(1)求A、B两种商品的销售单价;
(2)如果该商场计划最多投入2 000元用于购进A、B两种商品共80件,那么购进A种商品的件数应满足怎样的条件?
(3)现该商场对A、B两种商品进行优惠促销,优惠措施如表所示:
| 打折前一次性购物总金额 | 优惠措施 |
| 不超过500元 | 售价打九折 |
| 超过500元 | 售价打八折 |
分析 (1)根据商场销售5件A商品和1件B商品,可获得利润35元;销售6件A商品和3件B商品,可获得利润60元,分别得出等式求出答案;
(2)根据“商场计划最多投入2000元用于购进此两种商品共80件”列出不等式,解不等式求出其解;
(3)设到该商场购买甲种商品m件,购买乙种商品n件.分两种情况讨论:①打折前一次性购物总金额不超过500;②打折前一次性购物总金额超过500.
解答 解:(1)设甲商品售价为x元,则乙商品售价为y元,由题意,得
$\left\{\begin{array}{l}{5(x-15)+y-35=35}\\{6(x-15)+3(y-35)=60}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=20}\\{y=45}\end{array}\right.$,
答:甲商品售价为20元,则乙商品售价为45元
(2)由题意,得15x+35(80-x)≤2000,
解之,得x≥40.
故购进A种商品的件数不应低于40件;
(3)设到该商场购买甲种商品m件,购买乙种商品n件.
①当打折前一次性购物总金额不超过500时,购物总金额为432÷0.9=480(元),
则20m+45n=480,m=24-$\frac{9}{4}$n>0,∴0<n<$\frac{32}{3}$.
n是4的倍数,有2种情况:
情况1:m=6,n=8,则利润是:432-8×35-6×15=62(元);
情况2:m=15,n=4,则利润是:432-(15×15+35×4)=67(元);
②当打折前一次性购物总金额超过500时,购物总金额为432÷0.8=540(元),
则20m+45n=540,m=27-$\frac{9}{4}$n≥0,∴0<n≤12.
m、n均是正整数,n是4的倍数,有2种情况:
情况1:m=9,n=8,则利润为:432-(9×15+8×35)=17(元);
情况2:m=18,n=4,则利润为:432-(18×15+4×35)=22(元);
综上所述,商家可获得的最小利润是17元,最大利润是67元.
点评 本题考查了一次函数的应用、一元一次不等式的运用,解答本题时求出一次函数的解析式,进行分类讨论是关键.

| A. | 正整数和负整数统称为整数 | B. | 有理数都可以用数轴上的点来表示 | ||
| C. | 符号不同的两个数叫做互为相反数 | D. | 两个有理数,绝对值大的反而小 |
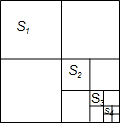 【阅读】求值:1+2+22+23+…+22016
【阅读】求值:1+2+22+23+…+22016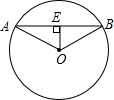 如图,在半径为6cm的⊙O中,圆心O到弦AB的距离OE为3cm.
如图,在半径为6cm的⊙O中,圆心O到弦AB的距离OE为3cm.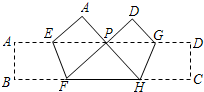 如图,把宽为3cm的纸条ABCD沿EF,GH同时折叠,B、C两点恰好落在AD边的P点处,若△PFH的周长为16cm,则长方形ABCD的面积为48cm2.
如图,把宽为3cm的纸条ABCD沿EF,GH同时折叠,B、C两点恰好落在AD边的P点处,若△PFH的周长为16cm,则长方形ABCD的面积为48cm2.