题目内容
14. 如图,△ABC和△AMN均为等边三角形,将△AMN绕点A旋转(△AMN在直线AC的右侧).
如图,△ABC和△AMN均为等边三角形,将△AMN绕点A旋转(△AMN在直线AC的右侧).(1)求证:△BAM≌△CAN;
(2)若点C,M,N在同一条直线上,
①求∠BMC的度数;
③点M是CN的中点,求证:BM⊥AC.
分析 (1)由等边三角形的性质得出AB=AC,AM=AN,∠BAC=∠MAN=60°,再证出∠BAM=∠CAN,由SAS即可证明△ABM≌△ACN.
(2)①由等边三角形的性质得出∠AMN=∠NAM=∠AMN=60°,由全等三角形的性质得出∠AMB=∠MNA=60°,再由平角定义即可得出结果;
②由等边三角形的性质证出MB是AC的垂直平分线,即可得出结论.
解答 (1)证明:∵△ABC和△AMN是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAC+∠MAC=∠MAN+∠MAC,
即∠BAM=∠CAN,
在△BAM和△CAN中,$\left\{\begin{array}{l}{AB=AC}&{\;}\\{∠BAM=∠CAN}&{\;}\\{AM=AN}&{\;}\end{array}\right.$,
∴△BAM≌△CAN;
(2)①解:∵△AMN为等边三角形,
∴∠AMN=∠NAM=∠AMN=60°,
∵△BAM≌△CAN,
∴∠AMB=∠MNA=60°,
∴∠BMC=180°-∠AMN-∠AMB=60°;
②证明:∵点M是CN的中点,
∴MN=CM,
∵△AMN是等边三角形,
∴AM=MN=CM,
∵△ABC为等边三角形,
∴AB=CB,
∴MB是AC的垂直平分线,
∴BM⊥AC.
点评 本题考查了等边三角形的性质、线段垂直平分线的性质、全等三角形的判定与性质、等腰三角形的判定与性质;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目

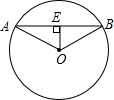 如图,在半径为6cm的⊙O中,圆心O到弦AB的距离OE为3cm.
如图,在半径为6cm的⊙O中,圆心O到弦AB的距离OE为3cm. 如图,点M是抛物线y=-$\frac{1}{2}$(x-1)2+4上在第一象限内的点,MN∥x轴交抛物线于点N,M在N的右边,P是x轴上一点,当△MNP是以MN为底的等腰直角三角形时,则点M的坐标是(3,2).
如图,点M是抛物线y=-$\frac{1}{2}$(x-1)2+4上在第一象限内的点,MN∥x轴交抛物线于点N,M在N的右边,P是x轴上一点,当△MNP是以MN为底的等腰直角三角形时,则点M的坐标是(3,2). 如图,将矩形ABCD绕点A顺时针旋转到矩形A′B′C′D′的位置,旋转角为α
如图,将矩形ABCD绕点A顺时针旋转到矩形A′B′C′D′的位置,旋转角为α