Question

18．如图，在⊙O中，弦AB=CD，且相交于点E，连接OE．
（1）如图1，求证：EO平分∠BEC；
（2）如图2，点F在半径OD的延长线上，连接AC、AF，当四边形ACDF是平行四边形时，求证：OE=DE；
（3）如图3，在（2）的条件下，AF切⊙O于点A，点H为弧BC上一点，连接AH、BH、DH，若BH=$\frac{2}{3}$AH，AB=$\sqrt{21}$，求DH的长．

Answer 1

分析 （1）作OH⊥CD，OM⊥AB，由AB=CD，根据垂径定理可知OH=OM，由到角的两边距离相等的点在角的平分线上可知，OE平分∠CEB，结论得以证明；
（2）要证OE=DE，只要证明∠EOD=∠EDO即可，根据题目中的条件可以证得两个角相等，从而可以证明结论成立；
（3）根据题意作出合适的辅助线，构造直角三角形，利用特殊角的三角函数，进行边角的转化，从而可以求得DH的长．

解答 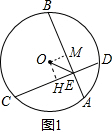（1）证明：过点O作OH⊥CD，OM⊥AB，垂足分别为H、M，如右图1所示，
∵AB=CD，
∴OH=OM，
∴EO平分∠BEC；
（2）连接OA、BD，如右图2所示，
∵AB=CD
∴$\widehat{AC}+\widehat{AB}=\widehat{CD}+\widehat{BD}$，
∴$\widehat{AC}=\widehat{BD}$
∴AC=BD，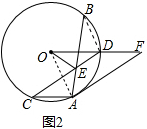
又∵∠DBE=∠ACE，∠CEA=∠BED，
∴△CEA≌△BED，
∴AE=DE，
又∵OE平分∠CEB，∠BED=∠CEA，
∴∠OEC=∠OEB，
∴∠OEA=∠OED，
∵OE=OE，
∴△AOE≌△DOE，
∴∠DOE=$\frac{1}{2}$∠DOA，
又∵四边形CAFD是平行四边形，
∴∠F=∠C=∠ODE，
∴∠C=$\frac{1}{2}$∠DOA=∠EOD=∠F=∠ODE，
∴∠EOD=∠EDO，
∴OE=DE；
（3）如图3所示，连接OA，则OA⊥AF，
∵四边形AFDC是平行四边形，
∴CD∥AF，
∴OA⊥CD，
∴$\widehat{AC}=\widehat{AD}=\widehat{BD}$，
∴OD⊥AB，
∵OE=DE，
∴OG=$\frac{1}{2}$OD=$\frac{1}{2}$AO，
∴∠AOD=60°，
∴∠AHB=∠AOD=60°，
过点A作AM⊥BH，则HM=$\frac{1}{2}$AH，AM=$\frac{\sqrt{3}}{2}$AH，
∴BM=BH-HM=$\frac{2}{3}$AH-$\frac{1}{2}$AH=$\frac{1}{6}$AH，
由勾股定理得，AB²=BM²+AM²，
即21=$\frac{1}{36}A{H}^{2}+\frac{3}{4}A{H}^{2}$，得AH=3$\sqrt{3}$，
∴BH=2$\sqrt{3}$，
∵OA=$\frac{AG}{sin60°}=\frac{\frac{\sqrt{21}}{2}}{\frac{\sqrt{3}}{2}}$=$\sqrt{7}$=BD，
过点B作BQ⊥DH于点Q，∠BHQ=30°，
∴BQ=$\sqrt{3}$，HQ=$2\sqrt{3}×\frac{\sqrt{3}}{2}$=3，
∴DQ=$\sqrt{B{D}^{2}-B{Q}^{2}}=\sqrt{（\sqrt{7}）^{2}-（\sqrt{3}）^{2}}$=2，
∴DH=HQ+DQ=3+2=5，
即DH=5．

点评 本题考查圆的综合题，解题的关键是明确题意，作出合适的辅助线，画出相应的图形，找出所求问题需要的条件，利用数形结合的思想和特殊角的三角函数值解答问题．