题目内容
19.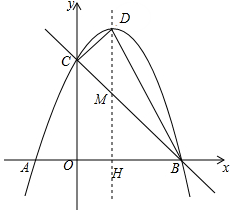 如图,已知抛物线y=-x2+bx+c轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于点P,与直线BC相交于点M,连接PB.
如图,已知抛物线y=-x2+bx+c轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于点P,与直线BC相交于点M,连接PB.(1)求该抛物线的解析式;
(2)在(1)中位于第一象限内的抛物线上是否存在点D,使得△BCD的面积最大?若存在,求出D点坐标及△BCD面积的最大值;若不存在,请说明理由.
(3)直线l经过A、C两点,点Q在抛物线位于y轴的左侧部分上运动,直线m经过点B和点Q是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.
分析 (1)由B、C两点的坐标,利用待定系数法可求得抛物线的解析式;
(2)设D(t,-t2+2t+3),过点D作DH⊥x轴,根据S△BCD=S梯形OCDH+S△BDH-S△BOC构建二次函数,利用二次函数的性质即可解决问题.
(3)设直线m与y轴交于点N,交直线l于点G,由于∠AGP=∠GNC+∠GCN,所以当△AGB和△NGC相似时,必有∠AGB=∠CGB=90°,则可证得△AOC≌△NOB,可求得ON的长,可求出N点坐标,利用B、N两的点坐标可求得直线m的解析式.
解答 解:(1)∵抛物线y=-x2+bx+c轴交于A(-1,0)、B(3,0)两点,
则有$\left\{\begin{array}{l}{-1-b+c=0}\\{-9+3b+c=0}\end{array}\right.$解得$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$,
∴抛物线的解析式为y=-x2+2x+3.
(2)设D(t,-t2+2t+3),过点D作DH⊥x轴, ,
,
则S△BCD=S梯形OCDH+S△BDH-S△BOC
=$\frac{1}{2}$(-t2+2t+3+3)t+$\frac{1}{2}$(3-t)(-t2+2t+3)-$\frac{1}{2}$×3×
3=-$\frac{3}{2}$t2+$\frac{9}{2}$t=-$\frac{3}{2}$(t-$\frac{3}{2}$)2+$\frac{27}{8}$
∵-$\frac{3}{2}$<0,
∴当t=-$\frac{\frac{9}{2}}{2×(-\frac{3}{2})}$=$\frac{3}{2}$时,D点坐标是($\frac{3}{2}$,$\frac{15}{4}$),△BCD面积的最大值是$\frac{27}{8}$.
(3)①如图,设直线m与y轴交于点N,交直线l于点G,由于∠AGP=∠GNC+∠GCN,所以当△AGB和△NGC相似时,必有∠AGB=∠CGB=90°,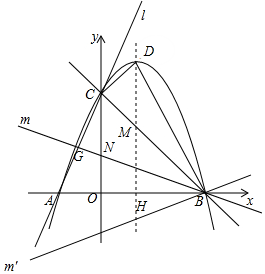
∵∠CNG=∠BNO,∠CGN=∠NOB=90°,
∴∠ACO=∠OBN,
在△AOC和△NOB中,
$\left\{\begin{array}{l}{∠ACO=∠OBN}\\{∠AOC=∠BON}\\{OC=OB}\end{array}\right.$,
∴△AOC≌△NOB,
∴ON=AO=1,
∴N(0,1),
设直线BG的解析式为y=kx+b,则有$\left\{\begin{array}{l}{b=1}\\{3k+b=0}\end{array}\right.$解得$\left\{\begin{array}{l}{k=-\frac{1}{3}}\\{b=1}\end{array}\right.$,
∴直线BG的解析式为y=-$\frac{1}{3}$x+1,
②当点Q在x轴上方时,此时直线m与①中的直线m关于x轴对称,
∴解析式为y=$\frac{1}{3}$x+1;
综上可知存在满足条件的直线m,其解析式为y=$\frac{1}{3}$x-1或y=-$\frac{1}{3}$x+1.
点评 本题为二次函数的综合应用,涉及知识点有待定系数法、二次函数的最值、相似三角形的判定、全等三角形的判定和性质等.在(2)中构建二次函数是解题的关键,在(3)中确定出满足条件的直线m的位置是解题的关键.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案| A. | 若x=y,则xm-5=ym-5 | B. | 若(a2+1)x=1,则x=$\frac{1}{{a}^{2}+1}$ | ||
| C. | 若x2=3x,则x=3 | D. | 若m=n,则am=an |
| 每回投球次数 | 30 | 60 | 90 | 150 | 200 | 300 | 400 | 500 |
| 每回进球次数 | 27 | 45 | 78 | 118 | 161 | 239 | 322 | 401 |
| 进球频率 | 0.900 | 0.750 | 0.867 | 0.787 | 0.805 | 0.797 | 0.805 | 0.802 |
(2)在比赛中该运动员因对手犯规获罚投篮一次,你能估计这次他能罚中的概率是多少吗?
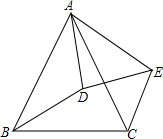 如图:已知∠BAC=∠DAE,∠ABD=∠ACE,BD=CE,求证:AB=AC.
如图:已知∠BAC=∠DAE,∠ABD=∠ACE,BD=CE,求证:AB=AC.