题目内容
3.在△ABC中,AD为高线,若AB+BD=CD,AC=4$\sqrt{5}$,BD=3,则线段BC的长度为5或11.分析 分两种情形①如图1中,△ABC是锐角三角形时.②如图2中,△ABC是钝角三角形时,分别利用勾股定理,列出方程即可解决问题.
解答 解:如图1中,设AB=x,则CD=AB+BD=3+x,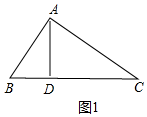
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴AD2=AB2-BD2=AC2-CD2,
∴x2-32=(4$\sqrt{5}$)2-(x+3)2,
解得x=5或-8(舍弃),
∴BC=BD+CD=3+3+5=11.
如图2中,设AB=x,则CD=AB+BD=3+x,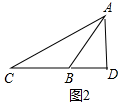
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴AD2=AB2-BD2=AC2-CD2,
∴x2-32=(4$\sqrt{5}$)2-(x+3)2,
解得x=5或-8(舍弃),
∴BC=CD-BD=5,
故答案为5或11.
点评 本题考查勾股定理的应用,解题的关键是学会用分类讨论的思想思考问题,注意有两种图形,学会构建方程解决问题,属于中考常考题型.

练习册系列答案
相关题目
18. 如图,多边形的相邻两边均互相垂直,则这个多边形的周长为( )
如图,多边形的相邻两边均互相垂直,则这个多边形的周长为( )
 如图,多边形的相邻两边均互相垂直,则这个多边形的周长为( )
如图,多边形的相邻两边均互相垂直,则这个多边形的周长为( )| A. | a+b | B. | 2a+b | C. | 2(a+b) | D. | a+2b |
13.某乡组织20辆汽车装运A、B、C三种苹果42吨到外地销售,按规定每辆车只装同一种苹果,且必须装满,每种苹果不少于2辆车.
(1)设用x辆车装运A种苹果,用y辆车装运B种苹果.根据上表提供的信息,求y与x之间的函数表达式,并写出自变量x的取值范围;
(2)设此次外销活动的利润为W元,求W与x之间的函数表达式及最大利润,并制定写出相应的车辆分配方案.
| 苹果品种 | A | B | C |
| 每辆汽车装载量/吨 | 2.2 | 2.1 | 2 |
| 每吨苹果获利/元 | 600 | 800 | 500 |
(2)设此次外销活动的利润为W元,求W与x之间的函数表达式及最大利润,并制定写出相应的车辆分配方案.
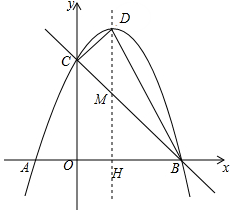 如图,已知抛物线y=-x2+bx+c轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于点P,与直线BC相交于点M,连接PB.
如图,已知抛物线y=-x2+bx+c轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于点P,与直线BC相交于点M,连接PB. 如图,已知矩形ABCD中,AB=4,AD=3,P是以CD为直径的半圆上的一个动点,连接BP.
如图,已知矩形ABCD中,AB=4,AD=3,P是以CD为直径的半圆上的一个动点,连接BP.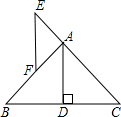 如图,在△ABC中,AB=AC,E在CA延长线上,AE=AF,AD是高,试判断EF与BC的位置关系,并说明理由.
如图,在△ABC中,AB=AC,E在CA延长线上,AE=AF,AD是高,试判断EF与BC的位置关系,并说明理由.