题目内容
2. 如图,四边形ABCD内接于⊙O,∠BAD=90°,$\widehat{BC}$=$\widehat{CD}$,过点C作CE⊥AD,垂足为E,若AE=3,DE=$\sqrt{3}$,求∠ABC的度数.
如图,四边形ABCD内接于⊙O,∠BAD=90°,$\widehat{BC}$=$\widehat{CD}$,过点C作CE⊥AD,垂足为E,若AE=3,DE=$\sqrt{3}$,求∠ABC的度数.
分析 作BF⊥CE于F,首先证得Rt△BCF≌Rt△CDE,从而判定四边形ABFE是矩形,然后利用锐角三角函数在Rt△CDE中求得∠D=60°,从而确定答案.
解答 解:作BF⊥CE于F,
∵∠BCF+∠DCE=90°,∠D+∠DCE=90°,
∴∠BCF=∠D.
又BC=CD,
∴Rt△BCF≌Rt△CDE.
∴BF=CE.
又∵∠BFE=∠AEF=∠A=90°,
∴四边形ABFE是矩形.
∴BF=AE.
∴AE=CE=3,
在Rt△CDE中
∵$tanD=\frac{CE}{DE}=\sqrt{3}$
∴∠D=60°
∵∠ABC+∠D=180°
∴∠ABC=120°.
点评 本题考查的是圆内接四边形的性质、圆周角定理,掌握圆内接四边形的对角互补是解题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目

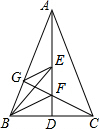 如图,在△ABC中,AD⊥BC于D,AB=AC,BE、BF将∠ABC三等分交AD于E、F,CF延长线交AB于G,求证:GE∥BF.
如图,在△ABC中,AD⊥BC于D,AB=AC,BE、BF将∠ABC三等分交AD于E、F,CF延长线交AB于G,求证:GE∥BF.
 如图,在矩形纸片ABCD中,AB=14,BC=8,点E为边BC上一点,且BE=5,将纸片沿过点E的一条直线l翻折,使点B落在直线CD上,若l与矩形的边的另一个交点为F,则EF的长为5$\sqrt{5}$.
如图,在矩形纸片ABCD中,AB=14,BC=8,点E为边BC上一点,且BE=5,将纸片沿过点E的一条直线l翻折,使点B落在直线CD上,若l与矩形的边的另一个交点为F,则EF的长为5$\sqrt{5}$. 如图,四边形ABCD是正方形,点F是BC的中点,FG⊥AF,点E在BC的延长线上,CG平分∠DCE,交FG于点G,AB=4,求CG.
如图,四边形ABCD是正方形,点F是BC的中点,FG⊥AF,点E在BC的延长线上,CG平分∠DCE,交FG于点G,AB=4,求CG.