题目内容
17. 如图,在矩形纸片ABCD中,AB=14,BC=8,点E为边BC上一点,且BE=5,将纸片沿过点E的一条直线l翻折,使点B落在直线CD上,若l与矩形的边的另一个交点为F,则EF的长为5$\sqrt{5}$.
如图,在矩形纸片ABCD中,AB=14,BC=8,点E为边BC上一点,且BE=5,将纸片沿过点E的一条直线l翻折,使点B落在直线CD上,若l与矩形的边的另一个交点为F,则EF的长为5$\sqrt{5}$.
分析 如图,连接B′F,EB′,作FG⊥CD于G.设BF′=CG=x,先在Rt△ECB′求出CB′,再在Rt△FGB′中利用勾股定理求出x,最后在Rt△BEF中 求出EF即可.
解答 解:如图,连接B′F,EB′,作FG⊥CD于G.设BF′=CG=x,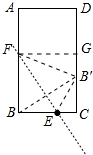
在Rt△EB′C中,∵EB′=EB=5,EC=3,
∴CB′=$\sqrt{EB{′}^{2}-E{C}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
在Rt△FGB′中,∵BF=FB′=x,FG=BC=8,FG=x-4,
∴x2=82+(x-4)2,
∴x=10.
∴BF=10,BE=5,
EF=$\sqrt{B{F}^{2}+B{E}^{2}}$=5$\sqrt{5}$,
故答案为5$\sqrt{5}$.
点评 本题考查翻折变换、矩形的先在、勾股定理等知识,解题的关键是灵活应用法则不变性结合勾股定理解决问题,属于中考常考题型.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
9.京东商城销售A、B两种型号的电风扇,销售单价分别为250元、180元,如表是近两周的销售利润情况:
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号电风扇的每台进价;
(2)若京东商城准备用不多于5万元的金额采购这两种型号的电风扇共300台,求A种型号的电风扇最多能采购多少台?
| 销售时段 | 销售数量 | 销售利润 | |
| A种型号 | B种型号 | ||
| 第一周 | 30台 | 60台 | 3300元 |
| 第二周 | 40台 | 100台 | 5000元 |
(1)求A、B两种型号电风扇的每台进价;
(2)若京东商城准备用不多于5万元的金额采购这两种型号的电风扇共300台,求A种型号的电风扇最多能采购多少台?

 如图,已知∠ACB=∠ABD=90°,CA=CB=6,∠DAB=30°,求以BD为直径的圆的面积.
如图,已知∠ACB=∠ABD=90°,CA=CB=6,∠DAB=30°,求以BD为直径的圆的面积.
 如图,四边形ABCD内接于⊙O,∠BAD=90°,$\widehat{BC}$=$\widehat{CD}$,过点C作CE⊥AD,垂足为E,若AE=3,DE=$\sqrt{3}$,求∠ABC的度数.
如图,四边形ABCD内接于⊙O,∠BAD=90°,$\widehat{BC}$=$\widehat{CD}$,过点C作CE⊥AD,垂足为E,若AE=3,DE=$\sqrt{3}$,求∠ABC的度数.