Question

20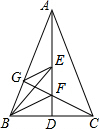．如图，在△ABC中，AD⊥BC于D，AB=AC，BE、BF将∠ABC三等分交AD于E、F，CF延长线交AB于G，求证：GE∥BF．

Answer 1

分析 设CG与BE交点为O，连接CE，根据等腰三角形的性质得到BD=DC，求得∠FCE=∠FBE=∠EBG，推出G，B，C，E四点共圆，由圆周角定理得到∠GEB=∠GCB，等量代换得到∠GEB=∠FBE，即可得证．

解答 证明：设CG与BE交点为O，连接CE，

∵AB=AC，AD⊥BC，
∴BD=DC，
∴FB=FC，
∴∠FBC=∠FCB，
同理∠EBC=∠ECB，
∴∠FBE=∠FCE，
∵BE，BF三等分∠GBD，
∴∠FCE=∠FBE=∠EBG，
∴G，B，C，E四点共圆，
∴∠GEB=∠GCB，
∴∠GEB=∠FBE，
∴GE∥BF．

点评 本题考查了平行线的判定和性质，四点共圆，等腰三角形的性质，正确的作出辅助线是解题的关键．