题目内容
3.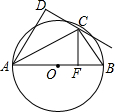 如图,AB是⊙O直径,C为⊙O上一点,AD垂直过C点的切线于点D,连接BC,过C点作CF⊥AB于点F.
如图,AB是⊙O直径,C为⊙O上一点,AD垂直过C点的切线于点D,连接BC,过C点作CF⊥AB于点F.(1)求证:CD=CF;
(2)若∠B=60°,CD=2$\sqrt{3}$,求⊙O的半径OB.
分析 (1)连接OC,如图,由切线的性质得OC⊥CD,加上CD⊥AD,则OC∥AD,再根据平行线的性质和等量代换可得到∠DAC=∠OAC,然后根据角平分线的性质定理得到结论;
(2)由(1)知,CF=CD=2$\sqrt{3}$,在Rt△BCF中利用正弦定义可计算出CB=4,再证明△OCB是等边三角形,于是得到OB=BC=4.
解答 (1)证明:连接OC,如图,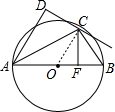
∵CD是⊙O切线,
∴OC⊥CD,
∵CD⊥AD,
∴OC∥AD,
∴∠DAC=∠ACO,
∵OA=OC,
∴∠ACO=∠OAC,
∴∠DAC=∠OAC,
∵CF⊥AB,CD⊥AD,
∴CD=CF;
(2)解:由(1)知,CF=CD=2$\sqrt{3}$,
在Rt△BCF中,∵sinB=$\frac{CF}{BC}$,
∴CB=$\frac{2\sqrt{3}}{sin60°}$=4,
∵OC=OB,∠B=60°,
∴△OCB是等边三角形,
∴OB=BC=4,
∴⊙O的半径为4.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.简记作:见切点,连半径,见垂直.

练习册系列答案
相关题目
13. 已知如图,△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60cm和38cm,则△ABC的腰和底边长分别为( )
已知如图,△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60cm和38cm,则△ABC的腰和底边长分别为( )
 已知如图,△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60cm和38cm,则△ABC的腰和底边长分别为( )
已知如图,△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60cm和38cm,则△ABC的腰和底边长分别为( )| A. | 24cm和12cm | B. | 16cm和22cm | C. | 20cm和16cm | D. | 22cm和16cm |
 已知二次函数y=x2+mx+n的图象经过点A(1,0)和D(4,3),与x轴的另一个交点为B,与y轴交于点C.
已知二次函数y=x2+mx+n的图象经过点A(1,0)和D(4,3),与x轴的另一个交点为B,与y轴交于点C.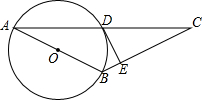 如图,AB为⊙O的直径,⊙O过AC的中点D,DE为⊙O的切线.
如图,AB为⊙O的直径,⊙O过AC的中点D,DE为⊙O的切线.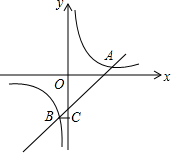 如图,在平面直角坐标系中,双曲线y=$\frac{m}{x}$和直线y=kx+b交于A,B两点,A(5,1),BC⊥y轴于C,且OC=5BC.
如图,在平面直角坐标系中,双曲线y=$\frac{m}{x}$和直线y=kx+b交于A,B两点,A(5,1),BC⊥y轴于C,且OC=5BC.