题目内容
15.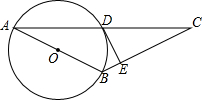 如图,AB为⊙O的直径,⊙O过AC的中点D,DE为⊙O的切线.
如图,AB为⊙O的直径,⊙O过AC的中点D,DE为⊙O的切线.(1)求证:DE⊥BC;
(2)如果DE=2,tanC=$\frac{1}{2}$,求⊙O的直径.
分析 (1)证明:连结OD,如图,先证明OD为△ABC的中位线得到OD∥BC,再根据切线的性质得到DE⊥OD,然后根据平行线的性质可判断DE⊥BC;
(2)连结BD,如图,先根据圆周角定理得到∠ADB=90°,再利用等角的余角相等得到∠C=∠BDE,接着根据正切的定义在Rt△CDE中计算出CE=2DE=4,在Rt△BDE中计算出BE=$\frac{1}{2}$DE=1,则BC=5,然后利用OD为△ABC的中位线可求出OD,从而得到圆的直径.
解答 (1)证明:连结OD,如图,
∵D为AC的中点,O为AB的中点,
∴OD为△ABC的中位线,
∴OD∥BC,
∵DE为⊙O的切线,
∴DE⊥OD,
∴DE⊥BC;
(2)解:连结BD,如图,
∵AB为直径,
∴∠ADB=90°,
∴∠BDE+∠CDE=90°,
而∠CDE+∠C=90°,
∴∠C=∠BDE,
在Rt△CDE中,∵tanC=$\frac{DE}{CE}$=$\frac{1}{2}$,
∴CE=2DE=4,
在Rt△BDE中,∵tan∠BDE=$\frac{BE}{DE}$=$\frac{1}{2}$,
∴BE=$\frac{1}{2}$DE=1,
∴BC=BE+CE=5,
∵OD为△ABC的中位线,
∴OD=$\frac{1}{2}$BC,
∴AB=BC=5,
即⊙O的直径为5.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.简记作:见切点,连半径,见垂直.

练习册系列答案
相关题目
6.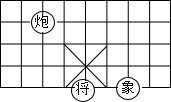 如图所示,若在某棋盘上建立直角坐标系,使“将”位于点(2,-2),“象”位于点(4,-2),则“炮”位于点( )
如图所示,若在某棋盘上建立直角坐标系,使“将”位于点(2,-2),“象”位于点(4,-2),则“炮”位于点( )
 如图所示,若在某棋盘上建立直角坐标系,使“将”位于点(2,-2),“象”位于点(4,-2),则“炮”位于点( )
如图所示,若在某棋盘上建立直角坐标系,使“将”位于点(2,-2),“象”位于点(4,-2),则“炮”位于点( )| A. | (1,3) | B. | (0,1) | C. | (-1,2) | D. | (-2,2) |
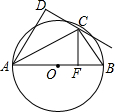 如图,AB是⊙O直径,C为⊙O上一点,AD垂直过C点的切线于点D,连接BC,过C点作CF⊥AB于点F.
如图,AB是⊙O直径,C为⊙O上一点,AD垂直过C点的切线于点D,连接BC,过C点作CF⊥AB于点F.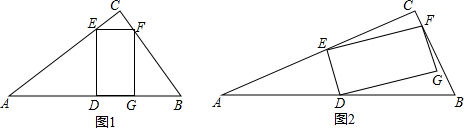
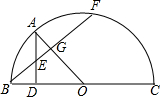 如图所示,BC是半圆O的直径,AD⊥BC,垂足为D,AB弧长等于AF弧长,BF与AD、AO分别交于点E、G.
如图所示,BC是半圆O的直径,AD⊥BC,垂足为D,AB弧长等于AF弧长,BF与AD、AO分别交于点E、G.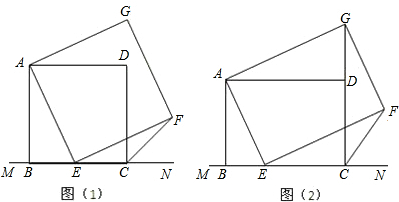
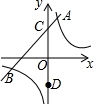 如图,一次函数y=x+3的图象与反比例函数y=$\frac{4}{x}$的图象交于A,B两点,与y轴交于点C,C点关于x轴的对称点是D点,则△ABD的面积是15.
如图,一次函数y=x+3的图象与反比例函数y=$\frac{4}{x}$的图象交于A,B两点,与y轴交于点C,C点关于x轴的对称点是D点,则△ABD的面积是15.