题目内容
18.先化简,后求值:($\frac{x+2}{{x}^{2}-2x}-\frac{x-1}{{x}^{2}-4x+4}$)$÷\frac{x-4}{x}$;x=5.分析 先通分,然后化除法为乘法、约分化简,最后代入求值.
解答 解:原式=[$\frac{x+2}{x(x-2)}$-$\frac{x-1}{(x-2)^{2}}$]×$\frac{x}{x-4}$,
=$\frac{{x}^{2}-4-{x}^{2}+x}{x(x-2)^{2}}$×$\frac{x}{x-4}$,
=$\frac{1}{(x-2)^{2}}$.
把x=5代入,则原式=$\frac{1}{(5-2)^{2}}$=$\frac{1}{9}$.
点评 本题考查了分式的化简求值.分式中的一些特殊求值题并非是一味的化简,代入,求值.许多问题还需运用到常见的数学思想,如化归思想(即转化)、整体思想等,了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助.就本节内容而言,分式求值题中比较多的题型主要有三种:转化已知条件后整体代入求值;转化所求问题后将条件整体代入求值;既要转化条件,也要转化问题,然后再代入求值.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
6.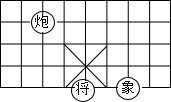 如图所示,若在某棋盘上建立直角坐标系,使“将”位于点(2,-2),“象”位于点(4,-2),则“炮”位于点( )
如图所示,若在某棋盘上建立直角坐标系,使“将”位于点(2,-2),“象”位于点(4,-2),则“炮”位于点( )
 如图所示,若在某棋盘上建立直角坐标系,使“将”位于点(2,-2),“象”位于点(4,-2),则“炮”位于点( )
如图所示,若在某棋盘上建立直角坐标系,使“将”位于点(2,-2),“象”位于点(4,-2),则“炮”位于点( )| A. | (1,3) | B. | (0,1) | C. | (-1,2) | D. | (-2,2) |
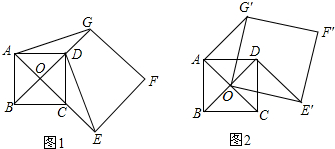
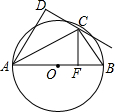 如图,AB是⊙O直径,C为⊙O上一点,AD垂直过C点的切线于点D,连接BC,过C点作CF⊥AB于点F.
如图,AB是⊙O直径,C为⊙O上一点,AD垂直过C点的切线于点D,连接BC,过C点作CF⊥AB于点F.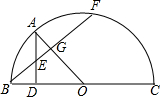 如图所示,BC是半圆O的直径,AD⊥BC,垂足为D,AB弧长等于AF弧长,BF与AD、AO分别交于点E、G.
如图所示,BC是半圆O的直径,AD⊥BC,垂足为D,AB弧长等于AF弧长,BF与AD、AO分别交于点E、G.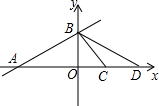 已知一次函数y=$\frac{{\sqrt{2}}}{3}$x+$\sqrt{2}$的图象与x轴,y轴,分别交于A、B两点,点C坐标为(1,0),点D在x轴上,且∠BCD和∠ABD是两个不相等的钝角,求经过B、D两点的一次函数的解析式.
已知一次函数y=$\frac{{\sqrt{2}}}{3}$x+$\sqrt{2}$的图象与x轴,y轴,分别交于A、B两点,点C坐标为(1,0),点D在x轴上,且∠BCD和∠ABD是两个不相等的钝角,求经过B、D两点的一次函数的解析式.