题目内容
8.一次函数经过点A(0,2)且与函数y=-x相交与点B,已知点B的横坐标是-1,求该一次函数的表达式.分析 先根据正比例函数y=-x的图象相交于点B,点B的横坐标为-1,求得B的纵坐标,然后把A、B的坐标代入y=kx+b,即可求得一次函数的表达式.
解答 解:∵函数y=-x图象经过点B,且点B的横坐标x=-1,
∴点B的纵坐标y=1,
∴点B(-1,1),
设一次函数解析式为:y=kx+b,
根据题意,将点A(0,2)、点B(-1,1)代入得:
$\left\{\begin{array}{l}{b=2}\\{-k+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$,
∴该一次函数解析式为:y=-x+2.
点评 本题考查了待定系数法求解析式,求得点B的坐标是待定系数求一次函数解析式的关键.

练习册系列答案
相关题目
16.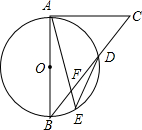 如图,AB为⊙O的直径,CA为⊙O的切线,CB交⊙O于D,$\widehat{AD}$=$\widehat{DE}$,AE交BD于F,若DF=BF,则tan∠BDE的值为( )
如图,AB为⊙O的直径,CA为⊙O的切线,CB交⊙O于D,$\widehat{AD}$=$\widehat{DE}$,AE交BD于F,若DF=BF,则tan∠BDE的值为( )
 如图,AB为⊙O的直径,CA为⊙O的切线,CB交⊙O于D,$\widehat{AD}$=$\widehat{DE}$,AE交BD于F,若DF=BF,则tan∠BDE的值为( )
如图,AB为⊙O的直径,CA为⊙O的切线,CB交⊙O于D,$\widehat{AD}$=$\widehat{DE}$,AE交BD于F,若DF=BF,则tan∠BDE的值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
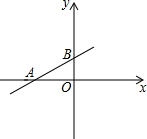 如图,一次函数y=kx+b图象经过点A(-4,0)和点B(0,2).
如图,一次函数y=kx+b图象经过点A(-4,0)和点B(0,2).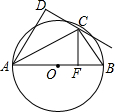 如图,AB是⊙O直径,C为⊙O上一点,AD垂直过C点的切线于点D,连接BC,过C点作CF⊥AB于点F.
如图,AB是⊙O直径,C为⊙O上一点,AD垂直过C点的切线于点D,连接BC,过C点作CF⊥AB于点F.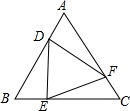 如图,等边△ABC中,点D、E、F分别同时从点A、B、C出发,以相同的速度在AB、BC、CA上运动,连结DE、EF、DF.
如图,等边△ABC中,点D、E、F分别同时从点A、B、C出发,以相同的速度在AB、BC、CA上运动,连结DE、EF、DF.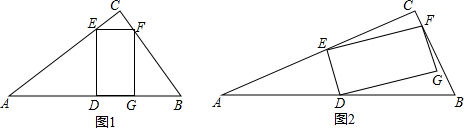
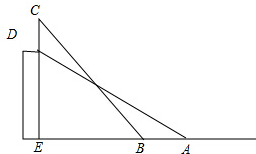 如图所示,某高校的教学大楼上竖有一根避雷针CD,小明为了知道避雷针CD的长度,在点A测得点D的仰角为30°,小明向大楼方向行进16m到达点B,又测得点C的仰角为45°,若大楼DE高度为24m,求避雷针CD的长度(结果保留根号).
如图所示,某高校的教学大楼上竖有一根避雷针CD,小明为了知道避雷针CD的长度,在点A测得点D的仰角为30°,小明向大楼方向行进16m到达点B,又测得点C的仰角为45°,若大楼DE高度为24m,求避雷针CD的长度(结果保留根号).