题目内容
13．现有一组数：-1，$\sqrt{23}$，0，5，求下列事件的概率：（1）从中随机选择一个数，恰好选中无理数；
（2）从中随机选择两个不同的数，均比0大．
分析 （1）直接根据概率公式求解；
（2）画树状图展示所有6种等可能的结果数，再找出“均比0大”的结果数，然后根据概率公式求解．
解答 解：（1）无理数为$\sqrt{23}$，从中随机选择一个数，恰好选中无理数的概率=$\frac{1}{4}$；
（2）画树状图为：
共有6种等可能的结果数，其中“均比0大”的结果数为2，
所以从中随机选择两个不同的数，均比0大的概率=$\frac{2}{12}$=$\frac{1}{6}$．
点评 本题考查了列表法与树状图法：利用列表法和树状图法展示所有可能的结果求出n，再从中选出符合事件A或B的结果数目m，求出概率．
练习册系列答案
阅读快车系列答案
相关题目
3．
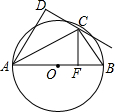如图，AB是⊙O直径，C为⊙O上一点，AD垂直过C点的切线于点D，连接BC，过C点作CF⊥AB于点F．
（1）求证：CD=CF；
（2）若∠B=60°，CD=2$\sqrt{3}$，求⊙O的半径OB．
如图，AB是⊙O直径，C为⊙O上一点，AD垂直过C点的切线于点D，连接BC，过C点作CF⊥AB于点F．（1）求证：CD=CF；
（2）若∠B=60°，CD=2$\sqrt{3}$，求⊙O的半径OB．
1．关于x的一元二次方程（k-1）x2-2x-（k-1）=0的根的判别式的值是4，则（ ）
| A． | k=-1 | B． | k=1 | C． | k=±1 | D． | k≠0 |
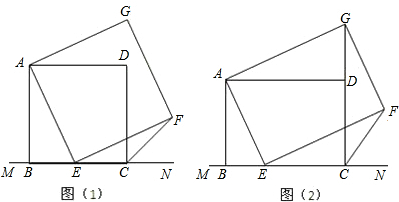
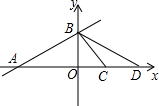已知一次函数y=$\frac{{\sqrt{2}}}{3}$x+$\sqrt{2}$的图象与x轴，y轴，分别交于A、B两点，点C坐标为（1，0），点D在x轴上，且∠BCD和∠ABD是两个不相等的钝角，求经过B、D两点的一次函数的解析式．
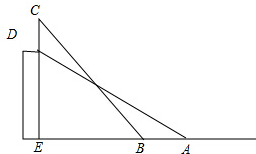如图所示，某高校的教学大楼上竖有一根避雷针CD，小明为了知道避雷针CD的长度，在点A测得点D的仰角为30°，小明向大楼方向行进16m到达点B，又测得点C的仰角为45°，若大楼DE高度为24m，求避雷针CD的长度（结果保留根号）．
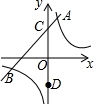如图，一次函数y=x+3的图象与反比例函数y=$\frac{4}{x}$的图象交于A，B两点，与y轴交于点C，C点关于x轴的对称点是D点，则△ABD的面积是15．