题目内容
12.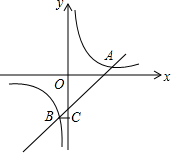 如图,在平面直角坐标系中,双曲线y=$\frac{m}{x}$和直线y=kx+b交于A,B两点,A(5,1),BC⊥y轴于C,且OC=5BC.
如图,在平面直角坐标系中,双曲线y=$\frac{m}{x}$和直线y=kx+b交于A,B两点,A(5,1),BC⊥y轴于C,且OC=5BC.(1)求双曲线和直线的解析式;
(2)若点P是x轴上一点,且满足△ABP是以AB为直角边的直角三角形,请直接写出点P的坐标.
分析 (1)先把A点坐标代入y=$\frac{m}{x}$求出m,从而得到反比例函数解析式;再利用OC=6BC可设B点坐标为(t,-6t)(t>0),然后把B(t,-6t)代入反比例函数解析式求出t,得到B点坐标为(1,-6),再利用待定系数法求一次函数解析式;
(2)根据直线AB的解析式和题意设出另一条直角边的解析式,然后分两种情况分别讨论即可求得P的坐标.
解答 解:(1)∵A(5,1)在反比例y=$\frac{m}{x}$图象上,
∴m=5×1=5,
∴反比例函数解析式为y=$\frac{5}{x}$;
∵BC⊥y轴于点C,且OC=5BC,
∴设B点坐标为(-t,-5t)(t>0),
把B(-t,-5t)代入y=$\frac{5}{x}$得t1=1,t2=-1(舍去),
∴B点坐标为(-1,-5),
把A(5,1)、B(-1,-5)代入y=kx+b得$\left\{\begin{array}{l}{5k+b=1}\\{-k+b=-5}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=-4}\end{array}\right.$.
∴一次函数解析式为y=x-4;
(2)∵点P是x轴上一点,且满足△ABP是以AB为直角边的直角三角形,AB的解析式为y=x-4,
∴设另一条直角边的解析式为y=-x+n,
当直角顶点是A时,则有1=-5+n,解得n=6,
∴解析式为y=-x+6,
令y=0,则x=6,
当直角顶点是B时,则有-5=1+n,解得n=-6,
∴解析式为y=-x-6,
令y=0,则x=-6,
∴点P的坐标是(6,0)或(-6,0).
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式.

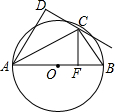 如图,AB是⊙O直径,C为⊙O上一点,AD垂直过C点的切线于点D,连接BC,过C点作CF⊥AB于点F.
如图,AB是⊙O直径,C为⊙O上一点,AD垂直过C点的切线于点D,连接BC,过C点作CF⊥AB于点F.(1)求证:CD=CF;
(2)若∠B=60°,CD=2$\sqrt{3}$,求⊙O的半径OB.
| A. | k=-1 | B. | k=1 | C. | k=±1 | D. | k≠0 |
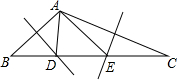 如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.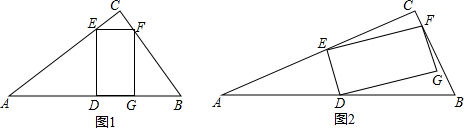
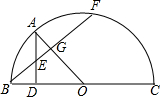 如图所示,BC是半圆O的直径,AD⊥BC,垂足为D,AB弧长等于AF弧长,BF与AD、AO分别交于点E、G.
如图所示,BC是半圆O的直径,AD⊥BC,垂足为D,AB弧长等于AF弧长,BF与AD、AO分别交于点E、G.