题目内容
6. 如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和点B(b,0),交y轴于点C,抛物线的顶点为D.下列四个判断:
如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和点B(b,0),交y轴于点C,抛物线的顶点为D.下列四个判断:①当x>0时,y>0;
②若a=-1,则b=4;
③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;
④若AB>2,则m<-1.
其中正确判断的序号是( )
| A. | ① | B. | ② | C. | ③ | D. | ④ |
分析 利用函数图象找出图象在x轴上方所对应的自变量的取值范围对①进行判断;先确定抛物线的对称性对②进行判断;根据二次函数的性质对③进行判断;利用根与系数的关系用m表示AB,从而得到关于m的不等式,然后解不等式可对④进行判断.
解答 解:当a<x<b时,y>0,所以①错误;
抛物线的对称轴为直线x=-$\frac{2}{2×(-1)}$=1,而A(-1,0),所以B点坐标为(3,0),所以②错误;
因为x1<1<x2,且x1+x2>2,则点Q到直线x=1的距离比点P到直线x=1的距离大,所以y1>y2,所以③正确;
因为a+b=2,ab=-(m+1),所以AB=$\sqrt{(b-a)^{2}}$=$\sqrt{(a+b)^{2}-4ab}$=$\sqrt{{2}^{2}+4(m+1)}$>2,解得m>-1,所以④错误.
故选C.
点评 本题考查了抛物线与x轴的交点:由二次函数的交点式y=a(x-x1)(x-x2)(a,b,c是常数,a≠0)可直接得到抛物线与x轴的交点坐标(x1,0),(x2,0).也考查了根与系数的关系.

练习册系列答案
相关题目
17. 将等腰Rt△ABC绕点A逆时针旋转15°得到△AB′C′,若AC=1,则图中阴影部分面积为( )
将等腰Rt△ABC绕点A逆时针旋转15°得到△AB′C′,若AC=1,则图中阴影部分面积为( )
 将等腰Rt△ABC绕点A逆时针旋转15°得到△AB′C′,若AC=1,则图中阴影部分面积为( )
将等腰Rt△ABC绕点A逆时针旋转15°得到△AB′C′,若AC=1,则图中阴影部分面积为( )| A. | $\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{6}$ |
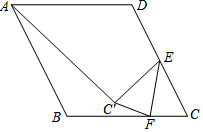 如图,菱形ABCD中,AB=4,∠B=120°,点E为CD的中点,F为BC边上一动点,将△EFC延EF折叠得到△EFC′,连接AC′,则AC′的最小值为2$\sqrt{7}$-2.
如图,菱形ABCD中,AB=4,∠B=120°,点E为CD的中点,F为BC边上一动点,将△EFC延EF折叠得到△EFC′,连接AC′,则AC′的最小值为2$\sqrt{7}$-2. 如图,已知菱形ABCD的面积为96,对角线AC,BD相交于点O,AC=16,则菱形ABCD的周长为40.
如图,已知菱形ABCD的面积为96,对角线AC,BD相交于点O,AC=16,则菱形ABCD的周长为40. 如图,E、F是平行四边形ABCD对角线AC上的点,且BE∥DF,求证:△ABE≌△CDE.
如图,E、F是平行四边形ABCD对角线AC上的点,且BE∥DF,求证:△ABE≌△CDE.