题目内容
11. 如图,已知菱形ABCD的面积为96,对角线AC,BD相交于点O,AC=16,则菱形ABCD的周长为40.
如图,已知菱形ABCD的面积为96,对角线AC,BD相交于点O,AC=16,则菱形ABCD的周长为40.
分析 根据菱形对角线互相垂直平分的性质,可以求得BO=OD,AO=OC,在Rt△AOB中,根据勾股定理可以求得AB的长,即可求得菱形ABCD的周长.
解答 解:∵四边形ABCD是菱形,
∴BO=OD=$\frac{1}{2}$BD,AO=OC=$\frac{1}{2}$AC=8,AC⊥BD,AB=BC=CD=AD,
∴$\frac{1}{2}$AC•BD=96,
∴BD=12,
∴BO=6,
∴AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10,
∴菱形的周长=4×10=40.
故答案为:40.
点评 本题考查了勾股定理、菱形的性质以及菱形面积和周长的计算;熟练掌握菱形的性质和勾股定理是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.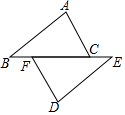 如图,点B、F、C、E在一条直线上,AB∥ED,AB=DE,要使△ABC≌△DEF,需要添加下列选项中的一个条件是( )
如图,点B、F、C、E在一条直线上,AB∥ED,AB=DE,要使△ABC≌△DEF,需要添加下列选项中的一个条件是( )
 如图,点B、F、C、E在一条直线上,AB∥ED,AB=DE,要使△ABC≌△DEF,需要添加下列选项中的一个条件是( )
如图,点B、F、C、E在一条直线上,AB∥ED,AB=DE,要使△ABC≌△DEF,需要添加下列选项中的一个条件是( )| A. | BF=EC | B. | AC=DF | C. | ∠B=∠E | D. | BF=FC |
20.在△ABC中和△DEF中,已知AC=DF,∠C=∠F,增加下列条件后还不能判定△ABC≌△DEF的是( )
| A. | BC=EF | B. | AB=DE | C. | ∠A=∠D | D. | ∠B=∠E |
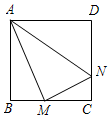 如图,正方形ABCD边长为8,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,始终保持AM和MN垂直,设BM=x,梯形ABCN的面积为y.
如图,正方形ABCD边长为8,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,始终保持AM和MN垂直,设BM=x,梯形ABCN的面积为y. 如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和点B(b,0),交y轴于点C,抛物线的顶点为D.下列四个判断:
如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和点B(b,0),交y轴于点C,抛物线的顶点为D.下列四个判断: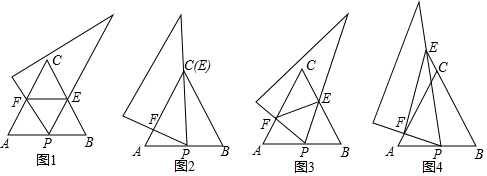

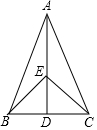 如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.