题目内容
16.已知直线l1:y1=x+m与直线l2:y2=nx+3相交于点A(1,2).(1)求m、n的值;
(2)设l1交x轴于点B,l2交x轴于点C,若点D与点A、B、C能构成平行四边形,请直接写出D点坐标.
分析 (1)由于两直线交于点A,所以可将点A代入两直线中即可求出m、n的值.
(2)根据直线的解析式求出点B与C的坐标,然后根据平行四边形的性质即可求出答案.
解答 解:(1)将点A(1,2)代入y1=x+m,y2=nx+3,
2=1+m,2=n+3,
解得:m=1,n=-1.
(2)当y1=x+1=0时,x=-1,
∴点B(-1,0);
当y2=-x+3=0时,x=3,
∴点C(3,0).
当AC为对角线时,点D1(1+3-(-1),2+0-0),即(5,2);
当AB为对角线时,点D2(1+(-1)-3,2+0-0),即(-3,2);
当BC为对角线时,点D3(3+(-1)-1,0+0-2),即(1,-2).
故若点D与点A、B、C能构成平行四边形,D点坐标为(5,2)、(-3,2)或(1,-2).
点评 本题考查了两条直线相交或平行问题、一次函数图象上点的坐标特征以及平行四边形的性质,解题的关键是(1)利用待定系数法求出m与n的值;(2)根据平行四边形的性质找出点D的坐标.

练习册系列答案
相关题目
5.若|a|=4,|b|=5,且ab<0,则a+b的值是( )
| A. | 1 | B. | -9 | C. | 9或-9 | D. | 1或-1 |
1.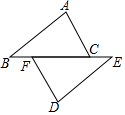 如图,点B、F、C、E在一条直线上,AB∥ED,AB=DE,要使△ABC≌△DEF,需要添加下列选项中的一个条件是( )
如图,点B、F、C、E在一条直线上,AB∥ED,AB=DE,要使△ABC≌△DEF,需要添加下列选项中的一个条件是( )
 如图,点B、F、C、E在一条直线上,AB∥ED,AB=DE,要使△ABC≌△DEF,需要添加下列选项中的一个条件是( )
如图,点B、F、C、E在一条直线上,AB∥ED,AB=DE,要使△ABC≌△DEF,需要添加下列选项中的一个条件是( )| A. | BF=EC | B. | AC=DF | C. | ∠B=∠E | D. | BF=FC |
8. 某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
 某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )| A. | 该村人均耕地面积随总人口的增多而增多 | |
| B. | 当该村总人口为50人时,人均耕地面积为1公顷 | |
| C. | 若该村人均耕地面积为2公顷,则总人口有100人 | |
| D. | 该村人均耕地面积y与总人口x成正比例 |
 在△ABC中,AD⊥BC于点D,BD=8,AD=6,S△ABC=42,那么AC的长为6$\sqrt{2}$.
在△ABC中,AD⊥BC于点D,BD=8,AD=6,S△ABC=42,那么AC的长为6$\sqrt{2}$. 在平面直角坐标系中,点A(0,6),B(8,0),AB=10,如图作∠DBO=∠ABO,∠CAy=∠BAO,直线CD过点O.
在平面直角坐标系中,点A(0,6),B(8,0),AB=10,如图作∠DBO=∠ABO,∠CAy=∠BAO,直线CD过点O. 如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和点B(b,0),交y轴于点C,抛物线的顶点为D.下列四个判断:
如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和点B(b,0),交y轴于点C,抛物线的顶点为D.下列四个判断: