Question

1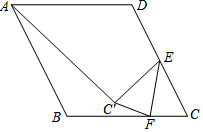．如图，菱形ABCD中，AB=4，∠B=120°，点E为CD的中点，F为BC边上一动点，将△EFC延EF折叠得到△EFC′，连接AC′，则AC′的最小值为2$\sqrt{7}$-2．

Answer 1

分析 AE、C′E的长度为定值，知当点C′在AE上时，AC′最小，过点E作EG⊥AD交AD的延长线于点G，利用菱形的性质得出AD=CD=AB=4、∠EDG=60°，由点E为CD的中点、△EFC延EF折叠得到△EFC′知CE=DE=C′E=2，利用三角函数得DG=DEcos∠EDG=1、EG=DEsin∠EDG=$\sqrt{3}$、AG=AD+DG=5，根据勾股定理得AE，从而由AC′=AE-C′E得出答案．

解答 解：如图，
∵AE、C′E的长度为定值，
∴当点C′在AE上时，AC′最小，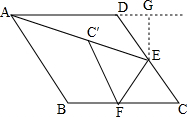

过点E作EG⊥AD交AD的延长线于点G，
∵四边形ABCD是菱形，∠B=120°、AB=4，
∴∠ADE=120°，AD=CD=AB=4，
∴∠EDG=60°，
∵点E为CD的中点，△EFC延EF折叠得到△EFC′，
∴CE=DE=C′E=2，
∵在Rt△DEG中，DG=DEcos∠EDG=2×$\frac{1}{2}$=1，EG=DEsin∠EDG=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$，
∴AG=AD+DG=4+1=5，
∴AE=$\sqrt{A{G}^{2}+E{G}^{2}}$=$\sqrt{{5}^{2}+（\sqrt{3}）^{2}}$=2$\sqrt{7}$，
则AC′=AE-C′E=2$\sqrt{7}$-2，
故答案为：2$\sqrt{7}$-2．

点评 此题主要考查了菱形的性质以及锐角三角函数关系等知识，得出A′点位置是解题关键．